- Preorden total
-
Preorden total
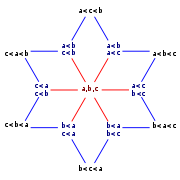Las 13 posibles preordenes totales en un conjunto de 3 elementos {a,b,c}. El único conjunto parcialmente ordenado esta coloreado, mientras que los totalmente ordenados están en negro. Dos órdenes se muestran conectadas por un vértice si difieren en la presencia o ausencia de un par simple en las relaciones definiendo los ordenamientos.
En teoría del orden , un preorden total sobre un conjunto X es un preorden ≤ sobre X que es total; es decir, que para cada par de elementos a y b en X, se cumple a ≤ b o bien b ≤ a.
La diferencia entre un preorden total y un orden total es que un preorden total (por ser preorden) NO tiene que ser antisimétrica.
Por ejemplo (X, ≤) para X = {1, 2} y a ≤ b para todo a y b en X.
Propiedades
Un preorden total debe satisfacer las siguientes propiedades. Para todo x e y en S,
- Para todo x, no es el caso que x < x(irreflexibilidad).
- Para todo x ≠ y, si x < y entonces NO es el caso de y < x (consultar antisimétrica).
- Para todo x, y y z', si x < y y y < z entonces x < z (transitividad).
- Para todo x, y y z, si x no es comparable con y, e y es incomparable con z, entonces x es incomparable con z (transitividad de equivalencia).
Es notable como la lista de propiedades es redundante, ya que la antisimetría sigue fácilmente desde la irreflexibilidad y transitividad.
La transitividad de equivalencia puede ser declarada de la siguiente manera:
- Si x < y, entonces para todo z, o bien x < z o z < y(o ambas).
Categoría: Teoría del orden
Wikimedia foundation. 2010.
