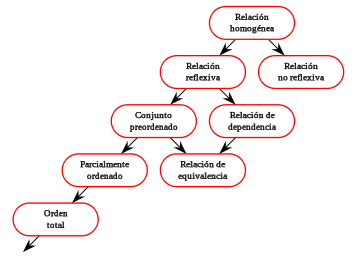
- Conjunto preordenado
-
En matemática, especialmente en teoría del orden, preórdenes son ciertas clases de relaciones binarias que se relacionan con los conjuntos parcialmente ordenados. El nombre quasiorden es también una expresión común para preórdenes. Muchas definiciones teóricas para los conjuntos parcialmente ordenados se pueden generalizar a preórdenes, pero el esfuerzo adicional de generalización raramente se necesita. Con todo hay campos de uso, tales como la definición de la convergencia vía redes en topología, donde los preórdenes no se pueden substituir por conjuntos parcialmente ordenados sin perder propiedades importantes.
Definición formal
Considere algún conjunto P y una relación binaria ≤ en P. Entonces ≤ es un preorden, o un cuasiorden, si es reflexiva y transitiva, es decir, para todo a, b y c en P, tenemos que:- a ≤ a (reflexividad)
- si a ≤ b y b ≤ c entonces a ≤ c (transitividad)
Un conjunto que se equipa con un preorden se llama un conjunto preordenado. Si un preorden es también antisimétrico, es decir, a ≤ b y b ≤ a implica a = b, entonces es un orden parcial.
Un orden parcial se puede construir con cualquier preorden identificando puntos "iguales". Formalmente, se define una relación de equivalencia ~ sobre X tal que a ~ b si y sólo si a ≤ b y b ≤ a. Ahora el conjunto cociente X/~, es decir el conjunto de todas las clases de equivalencia de ~, pueden ser fácilmente ordenadas definiendo [x] ≤ [y] si y sólo si x ≤ y. Por la construcción de ~ esta definición es independiente de los representantes elegidos y la relación correspondiente está de hecho bien definida. Se verifica fácilmente que esto da un conjunto parcialmente ordenado.
Esquema de temas relacionados
Teoría del orden Bien ordenado Orden total Parcialmente ordenado Preordenado Relación reflexiva Relación transitiva Relación antisimétrica Relación total Relación bien fundada Categorías:- Teoría del orden
- Conjuntos
Wikimedia foundation. 2010.