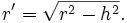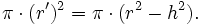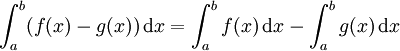El principio de Cavalieri ilustrado con monedas.

El Principio de Cavalieri (denominado en honor a su descubridor Bonaventura Cavalieri en el siglo XVII) es una ley geométrica que enuncia que la diferencia de volumen en dos cuerpos. El enunciado podría ser: "Si dos cuerpos tienen la misma altura y además tienen igual área en sus secciones planas realizadas a una misma altura, poseen entonces: igual volumen". Hoy en día en la moderna teoría de geometría analítica el principio de cavalieri es tomado como uncaso especial del Principio de Fubini. Cavalieri no hizo un uso extensivo del principio, empleándolo sólo en su Método de las indivisibles que expone en el año 1635 con la publicación de su obra Geometria indivisibilibus y también aparece en 1647 en su Exercitationes Geometricae. Antes del principio siglo XVII sólo se podría calcular el volumen de algunos cuerpos especiales ya tratados geométricamente por los resultados obtenidos por el griego Arquímedes y Kepler. La idea del cálculo de volúmenes mediante la comparación de secciones dio paso al desarrollo de los primeros pasos del cálculo infinitesimal así como de las integrales.

Ejemplos ilustrativos

Cilindro

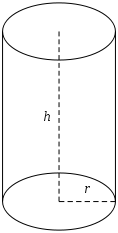
cilindro.

La sección de un cilindro proporciona un círculo si éste se hace perpendicular al eje de rotación principal del mismo, el área de dicha sección es πr², cuando r es el radio de la superficie (o de la parte interior el cilindro). Por el principio de Cavalieri el volumen del cilindro es igual al de un paralelepípedo cuando éste posee la misma altura h, siempre que la sección del paralepípedo tenga el mismo área y por lo tanto ambos poseen un volumen de .

Semiesfera

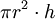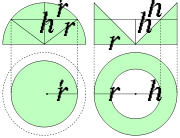
Sección vertical (superior) y horizontal (inferior) a través de una semiesfera.

La sección a lo largo de una semi-esfera de radio r muestra una superficie circular que si se realiza a una altura h paralela al horizonte, mediante el teorema de Pitágoras se obtiene un círculo de radio

Donde la superficie de la sección es por lo tanto

Cálculo de Integrales

Diferencia de la integral y diferencias de las integrales.

La idea tras el Principio de Cavalieri está muy relacionada con el cálculo integral. Un ejemplo de ello puede encontarse en el ejemplo de cálculo del perímetro de la sección de un plano con dos cuerpos, en el que se cumple la siguiente ecuación:

La relación se conoce ya que la superficie A₁ entre las dos funciones f y g son tan grandes como la superficie A₂ bajo la diferencia de fuciones 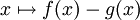; esta última superfice es perpendicular al cuerpo.

Referencias externas

• Ejemplo del cálculo del área de una esfera