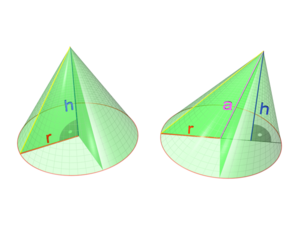
- Cono oblicuo
-
Un cono oblicuo es aquel cono cuyo eje de revolución no es perpendicular a su base.
Pueden ser de dos tipos: de base circular o de base elíptica. El de base elíptica es el cuerpo geométrico resultante de cortar un cono recto mediante un plano oblicuo a su eje de revolución.
Secciones de un cono recto y un cono oblicuo de base circular.
La base es un círculo o una elipse, y la altura es el segmento que contiene al vértice, siendo perpendicular al plano de la base; pero no es coincidente con el eje del cono.
Superficie y desarrollo
La superficie lateral de un cono oblicuo es un triángulo curvilíneo, con dos generatrices por lados y base semi-elíptica.
La superficie de la base de un cono oblicuo es un círculo o una elipse.
Volumen
La ecuación empleada para hallar el volumen de un cono oblicuo de base circular es similar a la del cono recto:
donde r es el radio de la base y h la altura del cono oblicuo.
La ecuación del volumen de un cono oblicuo de base elíptica es:siendo a y b los semiejes de la elipse y h la altura del cono oblicuo.
La justificación de las 2 fórmulas anteriores se basa en el principio de Cavalieri cuyo enunciado es el siguiente:"Si dos cuerpos tienen la misma altura y además tienen igual área en sus secciones planas realizadas a una misma altura, poseen entonces: igual volumen"
Categoría:- Figuras geométricas
-
Wikimedia foundation. 2010.
