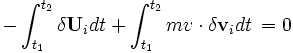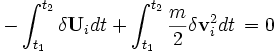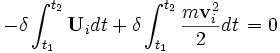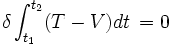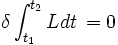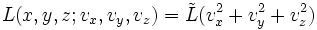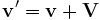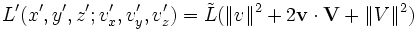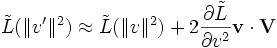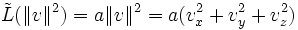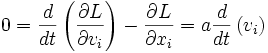- Principio de mínima acción
-
Principio de mínima acción
El principio de mínima o menor acción o principio de Hamilton es un presupuesto básico de la mecánica clásica y la mecánica relativista para describir la evolución a lo largo del tiempo del estado de movimiento de una partícula como de un campo físico. También en mecánica cuántica Feynman y Kac intentaron formulaciones inspiradas en el principio.[1]
Contenido
Historia
La primera formulación del principio se debe a Pierre-Louis Moreau de Maupertuis (1744), que dijo que la "naturaleza es económica en todas sus acciones" (D'Alembert había formulado un año antes el principio de d'Alembert que generalizaba las leyes de Newton). Entre los que desarrollaron la idea se incluyen Euler y Leibniz. Debe ser dicho que, desde el punto de vista del cálculo de variaciones, hablar de principio de acción estacionaria es más exacto. Anteriormente, Pierre de Fermat había introducido la idea de que los rayos de la luz, en situaciones ópticas tales como la refracción y la reflexión, seguían un principio de menor tiempo (ver principio de Fermat).
El principio de menor acción condujo al desarrollo de las formulaciones lagrangiana y hamiltoniana de la mecánica clásica. Aunque sean al principio más difíciles de captar, tienen la ventaja que su cosmovisión es más transferible a los marcos de la Teoría de la Relatividad y la mecánica cuántica que la de las leyes de Newton. Esto ha hecho pensar a alguna gente que este principio es un principio "profundo" de la física.
Formulación
La integral de acción para partículas
La formulación del principio para un sistema lagrangiano es fijado un sistema de coordenadas generalizadas sobre el espacio de configuración (o una parte del mismo, llamada carta local), de todas las trayectorias posibles que transcurren entre el instante t1 y t2, el sistema escogerá aquella que minimice la acción S. La magnitud acción viene dada para cada trayectoria por la integral:
Donde: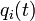 son las coordenadas paramétricas de una trayectoria posible.
son las coordenadas paramétricas de una trayectoria posible.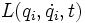 es la función lagrangiana del sistema.
es la función lagrangiana del sistema.
Ecuaciones de Euler-Lagrange para partículas
Puede probarse mediante principios variacionales, que de todas las trayectorias posibles, la que hace mínima (o, más bien, estacionaria) la anterior expresión es la que corresponde para todo i la siguiente ecuación:
Es decir, la variación de la integral temporal de la función lagrangiana es igual a cero. De esta ecuación se deducen asimismo las ecuaciones de Euler-Lagrange:
La integral de acción para campos
La formulación anterior es adecuada para partículas puntuales, o incluso sistemas mecánicos con un número finito de grados de libertad aunque no sean puntuales como un sólido rígido. Sin embargo para campos físicos que tienen una variación espacial o para la mecánica de medios continuos la formulación anterior no es adecuada y debe generalizarse.
La generalización más obvia es definir la acción como la integral de una función escalar, denominada densidad lagrangiana integrada sobre el volumen donde existe el campo o medio continuo:
En teoría clásica de campos es frecuente escribir la ecuación anterior de forma totalmente covariante:
Y en ese caso las ecuaciones de Euler-Lagrange resultan ser:
Principio de mínima acción y leyes de Newton
A partir de las leyes de Newton puede probarse el principio de mínima acción para partículas de la mecánica Newtoniana. Esta derivación puede hacerse a partir del principio de D'Alambert que es esencialmente equivalente a las leyes de Newton. Sin embargo, el principio de mínima acción es más general puesto que, a diferencia de las ecuaciones de Newton, es aplicable también a sistemas de referencia no inerciales.
Por otro lado admitiendo el principio de mínima acción de una sola partícula y ciertos principios de simetría pueden derivarse las ecuaciones de Newton. A continuación se presentan varias deducciones y ejemplos ilustrativos que muestran la equivalencia parcial de la mecánica newtoniana y el principio de mínima acción.
Principio de d'Alembert y segunda ley de Newton
En esta sección probaremos como a partir de la segunda ley de Newton o equivalentemente el principio de D'Alembert puede derivarse que para una partícula que obedece ese principio se cumple también el principio de mínima acción. Partiendo de la segunda ley se tiene que:
Esta forma es totalmente equivalente al principio de D'Alembert que establece que bajo cualquier desplazamiento virtual compatible con las ecuaciones de movimiento:
Como es bien sabido para una fuerza conservativa que deriva de un potencial se tiene que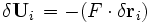 , es decir, la energía potencial
, es decir, la energía potencial 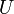 es igual al negativo del producto escalar de la fuerza por el desplazamiento del cuerpo. Reescribiendo la última ecuación introduciendo la definición de la aceleración:
es igual al negativo del producto escalar de la fuerza por el desplazamiento del cuerpo. Reescribiendo la última ecuación introduciendo la definición de la aceleración:
Procedemos a integrar por partes el segundo término del lado izquierdo de la ecuación: 1) aplicando la derivada temporal a la variación de la distancia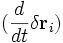 , en lugar de hacerlo a la velocidad
, en lugar de hacerlo a la velocidad 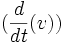 , y 2) introduciendo un término límite, que hace referencia a la diferencia del valor de la función
, y 2) introduciendo un término límite, que hace referencia a la diferencia del valor de la función ![\left[mv \cdot \delta{\mathbf r}_{i} \right]_{t_{1}}^{t_{2}}](/pictures/eswiki/101/efc28bfa10af018425ca0090d09dcb11.png) entre los puntos t2 y t1:
entre los puntos t2 y t1:
Los puntos de partida y de llegada de todas las trayectorias son los mismos, y por ello en esos lugares la variación es cero
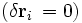 . Ello implica que la condición límite
. Ello implica que la condición límite ![\left[m{v_i} \cdot \delta{\mathbf r}_{i} \right]_{t_{1}}^{t_{2}}](/pictures/eswiki/57/904ff0eec7215b2b6bc491dcf9cd3e74.png) sea asimismo igual a cero en dichos lugares. Por ello, desaparece de la ecuación:
sea asimismo igual a cero en dichos lugares. Por ello, desaparece de la ecuación:
Procedemos a la integración de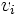 en el segundo término:
en el segundo término:
Las reglas del cálculo nos permiten trasladar los símbolos de la variación fuera de las dos integrales:
En esta ecuación están presentes las expresiones de la energía potencial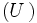 y la energía cinética
y la energía cinética 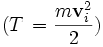 . Por lo tanto, puede reformularse de la siguiente manera:
. Por lo tanto, puede reformularse de la siguiente manera:
Donde la diferencia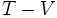 recibe el nombre de función lagrangiana y se representa con la letra
recibe el nombre de función lagrangiana y se representa con la letra 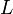 :
:
Primera ley de Newton y partícula libre
La primera ley de Newton puede deducirse a partir del principio de mínima acción de las propiedades de homogeneidad e isotropía del espacio euclídeo tridimensional. Para una partícula libre la función lagrangiana debido a las propiedades de homogeneidad del espacio no depende explícitamente de las coordenadas de posición. Igualmente debido a la isotropía, la dependencia en la velocidad de la partícula sólo puede depender del módulo al cuadrado de la velocidad. Eso nos lleva a que el lagrangiano debe ser de la forma:[2]
Si tomamos un sistema de referencia inercial K' que se mueve respecto al sistema anterior a una velocidad muy pequeña V, tenemos que la velocidad y el lagrangiano se transforman de acuerdo con las siguientes leyes:
Por tanto tendremos que para velocidades V pequeñas las formas funcionales de los dos lagrangianos están relacionadas por:
Como las trayectorias sólo pueden ser iguales si las dos funciones anteriores sólo difieren en una derivada total del tiempo, es necesario que exista una función de las coordenadas y del tiempo, tal que su derivada coincida con ese sumando. Eso sólo puede ocurrir si el segundo término es una función lineal de la velocidad cosa que sólo sucede si la derivada del segundo término se anula. Eso último a su vez requiere que:
Si introducimos esa forma del lagrangiano en las ecuaciones de Euler-Lagrange tenemos la primera ley de Newton:
Esta última ecuación dice que una partícula libre mantiene su velocidad constante.Principio de mínima acción y mecánica cuántica
"el movimiento del sistema entre los tiempos t1 y t2 es tal que el valor de la integral curvilínea.
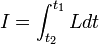
donde L=T-U es la lagrangiana, tiene un valor estacionario para el movimiento correcto".
A la integral J se le llama integral de acción.
Por valor estacionario entendemos que es aquel para el cual δJ=0, esto es, que el valor de la integral curvilínea cuando recorre el camino correcto no varía respecto de los caminos vecinos infinitesimalmente próximos (al menos, cuando estos infinitésimos son de primer orden).
Referencia
- Landau & Lifschitz: Mecánica, Ed. Reverté, Barcelona, 1991 (pp. 2-7) ISBN 84-291-4081-6.
Véase también
- Cálculo de variaciones
- Integración funcional
- Acción
Enlaces externos
Categorías: Principios y leyes físicas | Cálculo de variaciones
Wikimedia foundation. 2010.


![S\left[q_i,\dot{q}_i\right] = \int_{t_{1}}^{t_{2}} L(q_i(t), \dot{q}_i(t),t) dt](/pictures/eswiki/50/2c492f9035f5b18c58ff5fb5f7b23626.png)
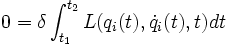
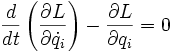
![S[\phi,\partial_t\phi,\partial_\mathbf{x}\phi] = \int_{t_{1}}^{t_{2}} dt \int_V \mathcal{L} (\phi(\mathbf{x},t), \partial_t\phi(\mathbf{x},t), \partial_\mathbf{x}\phi(\mathbf{x},t),\mathbf{x},t)\ d^3\mathbf{x}](/pictures/eswiki/55/768ba439a4025215c522cd14938afedf.png)
![\mathcal{S} [\phi_r^\alpha] = \int_R {\mathcal{L}(\mathbf{x}, \phi_r^\alpha, \partial_\mu \phi_r^\alpha) \ \mathrm{d}^4x}.](/pictures/eswiki/51/38a2490bf9d490c5b34bb84e709fad61.png)
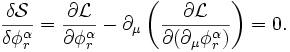
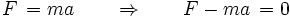
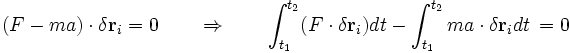
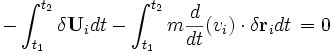
![- \int_{t_{1}}^{t_{2}} \delta{\mathbf U}_{i} dt + \int_{t_{1}}^{t_{2}} m{v_i} \cdot \frac{d}{dt}\delta{\mathbf r}_{i} dt \, - \left[m{v_i} \cdot \delta{\mathbf r}_{i} \right]_{t_{1}}^{t_{2}} = 0](/pictures/eswiki/99/c0df2bb01bf148966e3bec403f1f15eb.png)
![\left[m{v_i} \cdot \delta{\mathbf r}_{i} \right]_{t_{1}}^{t_{2}}\, = 0](/pictures/eswiki/55/7d749a7cb6502b347184ae529c131aa6.png)