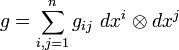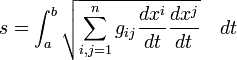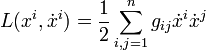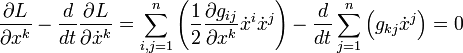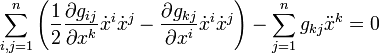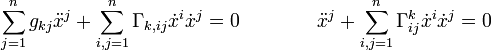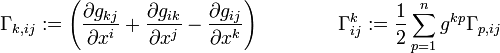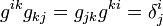Ecuaciones de Euler-Lagrange

Ecuaciones de Euler-Lagrange

Ecuaciones de Euler-Lagrange

Las ecuaciones de Euler-Lagrange son las condiciones bajo las cuales cierto tipo de problema variacional alcanza un extremo. Aparecen sobre todo en el contexto de la mecánica clásica en relación con el principio de mínima acción aunque también aparecen en teoría clásica de campos (electromagnetismo, Teoría general de la relatividad).

Contenido

Ecuaciones de Euler-Lagrange en física

Artículo principal: acción (física)

Caso unidimensional

En mecánica clásica, estas ecuaciones establecen que la integral de acción para un sistema físico es un mínimo. Donde la integral de acción viene dada por:

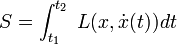
S = \int_{t_1}^{t_2}\; L(x,\dot{x}(t))dt

Y su correspondiente variación viene dada por:

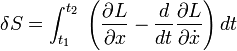
\delta S = \int_{t_1}^{t_2}\; \left( {\partial L\over \partial x} - {d\over dt }{\partial L\over\partial \dot x} \right)dt

Si se impone ahora que 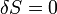\delta S =0\, para variaciones "cercanas", esto implica que: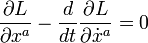

{\partial L\over\partial x^a} - {d\over dt }{\partial L\over\partial \dot{x}^a} = 0

donde L es el lagrangiano para el sistema, y xa son las coordenadas generalizadas del sistema.

Para una introducción a este tema:

Véase también: acción (física)

Caso multidimensional

La formalización de ciertos problemas físicos requiere construir una integral de acción sobre más de una variable. Así en teoría de campos y mecánica de medios continuos la acción física puede expresarse como una integral sobre un volumen:

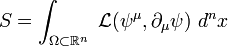
S = \int_{\Omega \subset \R^n} \; \mathcal{L}(\psi^\mu,\partial_\mu \psi) \ d^nx

Donde dnx es el elemento de volumen que usualmente viene dado por una n-forma y 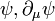\psi, \partial_\mu \psi representan las variables del campo y sus derivadas respecto a las coordenadas espaciales (o espacio-temporales). Cuando la acción toma esa forma las ecuaciones de Euler-Lagrange para el campo que minimiza la anterior integral, usando el convenio de sumación de Einstein, vienen dadas por: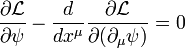

{\partial \mathcal{L}\over\partial \psi} - {d\over dx^\mu }{\partial \mathcal{L}\over\partial (\partial_\mu\psi)} = 0

Mecánica lagrangiana de la partícula

Teoría de campos

La teoría clásica de campos es un buen ejemplo del caso multidimensional anteriormente descrito. Así por ejemplo las ecuaciones de Maxwell no son otra cosa que las ecuaciones de Euler-Lagrange aplicadas al "lagrangiano" de Maxwell. La densidad lagrangiana de Maxwell viene dada por:

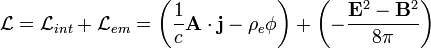
(*) \mathcal{L} = \mathcal{L}_{int} + \mathcal{L}_{em} = \left(\frac{1}{c} \mathbf{A}\cdot\mathbf{j}-\rho_e\phi\right)+ \left( -\frac{\mathbf{E}^2-\mathbf{B}^2}{8\pi}\right)

Donde el primer término es el lagrangiano de interacción y el segundo el lagrangiano del campo electromagnético libre y además:

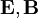\mathbf{E}, \mathbf{B}, son los campos eléctrico y magnético.
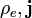\rho_e, \mathbf{j}, son la densidad de carga eléctrica y la densidad de corriente asociada a las cargas que interactúan con el campo.
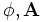\phi, \mathbf{A}, son el potencial eléctrico y el potencial vector del campo.

Considerando aquí el campo descrito por los potenciales 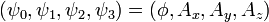(\psi_0, \psi_1, \psi_2, \psi_3) = (\phi, A_x, A_y, A_z)\,, los campos eléctrico y magnético son expresables en términos de sus derivadas: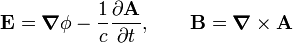

\mathbf{E} = \boldsymbol\nabla\phi - \frac{1}{c}\frac{\part \mathbf{A}}{\part t}, \qquad \mathbf{B} = \boldsymbol\nabla\times \mathbf{A}

Todos estos términos substituidos en la ecuación de Euler-Lagrange (*) nos lleva a las ecuaciones de Maxwell. Si a la densidad lagrangiana anterior le agregamos, la densidad lagrangiana de la materia en interacción con el campo electromagnético viene dado por:

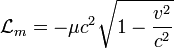
\mathcal{L}_{m}= -\mu c^2 \sqrt{1-\frac{v^2}{c^2}}

Cuando esta parte se tiene en cuenta también se recupera la expresión para la fuerza de Lorentz.

Aplicaciones en mecánica cuántica

Un artículo influyente, para la introducción del formalismo lagrangiano en la mecánica cuántica, fue el de Paul Dirac de 1932. El artículo titulado “El lagrangiano en Mecánica Cuántica” comienza de la siguiente manera:

“La mecánica cuántica fue construida sobre la base de la analogía con el hamiltoniano de la mecánica clásica. Esto se debe a que se encontró que la clásica noción de coordenadas canónicas y momentos es similar a la análoga cuántica, como resultado del cual la totalidad de la teoría clásica hamiltoniana, la cual es justamente una estructura construida sobre esta noción, debería ser tomada sobre todos sus detalles en mecánica cuántica.

Ahora tenemos una formulación alternativa para la dinámica clásica, provista por el lagrangiano. Esto requiere trabajar en términos de coordenadas y velocidades en lugar de coordenadas y momentos. Las dos formulaciones son, sin embargo, cercanamente relacionadas, pero hay razones para creer que el lagrangiano es el más fundamental.

En primer lugar, el método lagrangiano nos permite conectar juntas todas las ecuaciones del movimiento y expresarlas como una propiedad estacionaria de una cierta función de acción. (Esta función de acción es justamente la integral en el tiempo del lagrangiano). No existe un principio de acción correspondiente en términos de las coordenadas y momentos en la teoría hamiltoniana. En segundo lugar el método lagrangiano puede fácilmente ser expresado en forma relativista, teniendo en cuenta que la función de acción es invariante relativista; mientras que el método hamiltoniano es esencialmente de forma no relativista, dado que delimita una variable de tiempo particular como la conjugada canónica de la función hamiltoniana.

Por estas razones sería deseable tomar la cuestión de lo que corresponde en la teoría cuántica al método lagrangiano de la teoría clásica. Una pequeña consideración muestra, sin embargo, que uno no puede esperar ser capaz de tomar las ecuaciones clásicas de Lagrange en una forma directa. Estas ecuaciones involucran derivadas parciales del lagrangiano respecto a las coordenadas y velocidades y no significa poder tener tales derivadas en mecánica cuántica.

El sólo proceso de diferenciación que puede realizarse respecto a las variables dinámicas de la mecánica cuántica es el que forma los corchetes de Poisson y este proceso conduce a la teoría hamiltoniana.

Debemos por lo tanto mirar nuestra teoría cuántica lagrangiana de una manera indirecta. Debemos intentar tomar las ideas de la teoría lagrangiana clásica, no las ecuaciones de la teoría clásica lagrangiana”.[1]

Síntesis de aplicaciones en física

Como se vio antes, es posible derivar las ecuaciones de la mecánica clásica como las del electromagnetismo a partir del lagrangiano respectivo introducido en las ecuaciones de Euler-Lagrange. Por ese camino, es posible ampliar el lagrangiano de Maxwell para obtener el lagrangiano de Dirac y así obtener, luego, la ecuación relativista de Dirac. También las ecuaciones de Schrödinger, de Klein-Gordon y de Proca pueden obtenerse por ese método.

Incluso es posible derivar las ecuaciones de Einstein, de la relatividad generalizada, a partir del lagrangiano de Hilbert-Einstein[2]

Ecuaciones de Euler-Lagrange en geometría

Las ecuaciones de Euler-Lagrange pueden ser usadas para encontrar fácilmente la ecuación de las curvas geodésicas en una variedad de Riemann o "espacio curvo". Para ello consideremos un conjunto de coordenadas (x1, ...xn) sobre una región abierta U de la variedad de Riemann VR donde el tensor métrico viene dado por la expresión:

g = \sum_{i,j=1}^n g_{ij} \ dx^i \otimes dx^j \,

Puesto que dados dos puntos cualquiera de VR las geodésicas son las líneas de mínima longitud entre ellos podemos plantear el siguiente problema variacional, para el cuadrado de la longitud de una curva:

s = \int_{a}^{b} \sqrt {\sum_{i,j=1}^n g_{ij} \frac{dx^i}{dt} \frac{dx^j}{dt}} \quad dt \,


La minimización de la expresión anterior al ser la raíz una función monótona, es equivalente a la minimización de una integral de acción donde el lagrangiano sea:

L(x^i,\dot{x}^i) = \frac{1}{2} \sum_{i,j=1}^n g_{ij} \dot{x}^i \dot{x}^j \,

De ahí que la ecuación diferencial de las geodésicas venga dada por:

{\partial L\over\partial x^k} - {d\over dt }{\partial L\over\partial \dot{x}^k} = {\sum_{i,j=1}^n \left( \frac{1}{2} \frac{\partial g_{ij}}{\partial x^k} \dot{x}^i \dot{x}^j \right )} - {d\over dt} \sum_{j=1}^n \left ( g_{kj} \dot{x}^j \right )= 0

La ecuación anterior de hecho puede, usando la simetría del tensor métrico, escribirse como:

\sum_{i,j=1}^n \left ( \frac{1}{2} \frac{\partial g_{ij}}{\partial x^k} \dot{x}^i \dot{x}^j -\frac{\partial g_{kj}}{\partial x^i} \dot{x}^i \dot{x}^j \right ) - \sum_{j=1}^n g_{kj} \ddot{x}^k = 0


Que en términos de los símbolos de Christoffel (de primera o segunda especie) sencillamente como:

\sum_{j=1}^n g_{kj} \ddot{x}^j + \sum_{i,j=1}^n \Gamma_{k,ij} \dot{x}^i \dot{x}^j = 0 \qquad \qquad \ddot{x}^j + \sum_{i,j=1}^n \Gamma_{ij}^k \dot{x}^i \dot{x}^j = 0


Donde se han definido los símbolos de Christoffel como a partir de las derivadas del tensor métrico y el tensor inverso del tensor métrico:

\Gamma_{k,ij} := \left (\frac{\partial g_{kj}}{\partial x^i} + \frac{\partial g_{ik}}{\partial x^j} -\frac{\partial g_{ij}}{\partial x^k} \right ) \qquad \qquad \Gamma_{ij}^k :=\frac{1}{2} \sum_{p=1}^n g^{kp}\Gamma_{p,ij}
g^{ik}g_{kj} = g_{jk}g^{ki} = \delta_j^i

Referencias

  1. ↑ “The lagrangian in quantum mechanics” de P.A.M. Dirac en “Quantum Electrodynamics” editado por Julian Schwinger – Dover Publications Inc. - ISBN 486-60444-6
  2. ↑ “Lagrangian Interaction” de Noel A. Doughty – Addison Wesley Publishing Co. – ISBN 0-201-41625-5

Véase también

Obtenido de "Ecuaciones de Euler-Lagrange"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Ecuaciones de Euler-Lagrange — Las ecuaciones de Euler Lagrange establecen que la integral de acción para un sistema físico es extremal, es decir si la variación es y pedir para variaciones cercanas será si y solamente si donde L es el lagrangiano para el sistema, y son las… …   Enciclopedia Universal

  • Leonhard Euler — Retrato de Leonhard Euler, pintado por Johann Georg Bruck …   Wikipedia Español

  • Joseph-Louis de Lagrange — Para otros usos de este término, véase Lagrange (desambiguación). Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas …   Wikipedia Español

  • Historia de las ecuaciones diferenciales — Una ecuación es una igualdad condicional que se cumple sólo para las soluciones de la misma. Así, en una ecuación algebraica como x – 2 = 0, la igualdad sólo se cumple para x = 2. En forma similar, una ecuación diferencial, constituida por… …   Wikipedia Español

  • Interpolación polinómica de Lagrange — En análisis numérico, el polinomio de Lagrange, llamado así en honor a Joseph Louis de Lagrange, es el polinomio que interpola un conjunto de puntos dado en la forma de Lagrange. Fue descubierto por Edward Waring en 1779 y redescubierto más tarde …   Wikipedia Español

  • Identidad de los cuatro cuadrados de Euler — Este artículo o sección tiene el primer párrafo que usa términos técnicos sin explicación para los lectores interesados en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los… …   Wikipedia Español

  • Principio de acción — Saltar a navegación, búsqueda Para otros usos de la palabra acción, véase Acción. En física, el principio de acción es una aserción sobre la naturaleza del movimiento o trayectoria de un objeto o más generalmente la evolución temporal de un… …   Wikipedia Español

  • Lagrangiano — En física, un lagrangiano es una función matemática a partir de la cual se pueden obtener la evolución temporal, las leyes de conservación y otras propiedades importantes de un sistema físico. De hecho, en física moderna el lagrangiano se… …   Wikipedia Español

  • Principio de mínima acción — Saltar a navegación, búsqueda En la imagen aparecen una carga positiva fija (en rojo) y un electrón libre (en azul). De todas las trayectorias posibles, ¿cuál escogerá el electrón? El principio de acción mínima determina que la trayectoria 1 será …   Wikipedia Español

  • Mecánica hamiltoniana — La mecánica hamiltoniana fue formulada en 1833 por William R. Hamilton. Como la mecánica lagrangiana, es una reformulación de la mecánica clásica. La mecánica hamiltoniana puede ser formulada por sí misma, usando los espacios simplécticos, sin… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”