Rotación

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas.
Puedes añadirlas así o avisar al autor principal del artículo en su página de discusión pegando: {{subst:Aviso referencias|Rotación}} ~~~~

Para otros usos de este término, véase Rotación de cultivos y Rotación estelar.

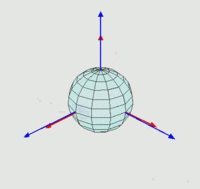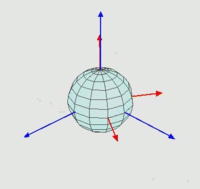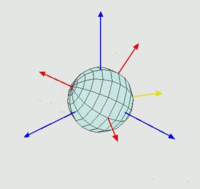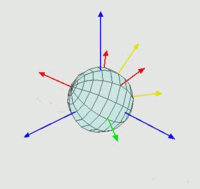
Rotación de la Tierra.

Rotación es el movimiento de cambio de orientación de un cuerpo o un sistema de referencia de forma que una línea (llamada eje de rotación) o un punto permanece fijo.

Una rotación de un cuerpo se representa mediante un operador que afecta a un conjunto de puntos o vectores. Un movimiento rotatorio se representa mediante el vector velocidad angular $\boldsymbol\omega$ , que es un vector de carácter deslizante, situado sobre el eje de rotación. Cuando el eje pasa por el centro de masa o de gravedad se dice que el cuerpo «gira sobre sí mismo».

La rotación también puede ser oscilatoria, como en el péndulo (izquierda). Los giros son completos sólo cuando la energía es lo suficientemente alta (derecha).

En ingeniería mecánica, se llama revolución a una rotación completa de una pieza sobre su eje (como en la unidad de revoluciones por minuto), mientras que en astronomía se usa esta misma palabra para referirse al movimiento orbital de traslación de un cuerpo alrededor de otro (como los planetas alrededor del Sol).

Contenido

1 Matemáticas
2 Parámetros de Euler-Rodrigues y cuaterniones
3 Concepto de rotación y revolución
4 Movimiento rotatorio
5 Teoría de grupos
- 5.1 Rotaciones frente a traslaciones
- 5.2 Rotaciones frente a reflexiones e inversiones
6 Percepción de las rotaciones
7 Véase también

Matemáticas

El tratamiento detallado de las rotaciones ha sido objeto de numerosos trabajos matemáticos, que abordan el problema desde diversos puntos de vista y grados de sofisticación: cuaterniones, matrices, operadores vectoriales, teoría de grupos... Todos estos enfoques son matemáticamente equivalentes y se pueden derivar unos de otros, salvo en algunos aspectos concretos y posibles resultados redundantes, y la elección de uno u otro depende del problema concreto. Con la llegada de la robótica y los gráficos informáticos, la matemática de las rotaciones ha cobrado un nuevo impulso y ha pasado a ser una materia de estudio muy activo, con particular énfasis en el enfoque basado en cuaterniones.

En matemáticas las rotaciones son transformaciones lineales que conservan las normas (es decir, son isométricas) en espacios vectoriales en los que se ha definido una operación de producto interior y cuya matriz tiene la propiedad de ser ortogonal y de determinante igual a ±1. Si el determinante es +1 se llama rotación propia y si es −1, además de una una rotación propia hay una inversión o reflexión y se habla de rotación impropia.

La conservación de la norma es equivalente a la conservación del producto interior, que se puede expresar como:

$\mathcal{R}\mathbf{a}\cdot\mathcal{R}\mathbf{b} =\mathbf{a}\cdot\mathbf{b}$

Consecuencia de ella es que las distancias y las formas también se conservan.

Como parámetro que determina la rotación se puede usar un vector (que tiene carácter deslizante) del eje de rotación y de longitud proporcional al ángulo de rotación. Sin embargo, lo normal es separar este vector en el ángulo y un vector unitario, lo que en el espacio da cuatro parámetros. Como consecuencia hay dos formas de representar una única rotación, pues

$\mathcal{R}(\theta,\mathbf{a}) = \mathcal{R}(-\theta,-\mathbf{a})$

Rotaciones en el plano

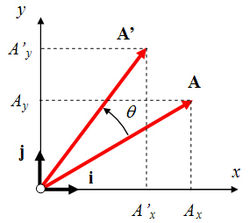
Cambio de base o rotación de un vector.

Sea un vector A en el plano cartesiano definido por sus componentes x e y, descrito vectorialmente a través de sus componentes:

$\mathbf A=\begin{bmatrix} A_x \\ A_y \end{bmatrix}$

La operación de rotación del punto señalado por este vector alrededor de un eje de giro puede siempre escribirse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector:

$\mathcal{R} \mathbf{A} = \mathbf{A}'$

En dos dimensiones la matriz de rotación para el vector dado puede escribirse de la manera siguiente:

$\mathcal{R} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{bmatrix}$

Al hacer la aplicación del operador, es decir, al multiplicar la matriz por el vector, obtendremos un nuevo vector A' que ha sido rotado en un ángulo $θ$ en sentido antihorario:

$\begin{bmatrix}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{bmatrix} \begin{bmatrix} A_x \\ A_y \end{bmatrix} = \begin{bmatrix} A'_x \\ A'_y \end{bmatrix}$

siendo

$A'_x = A_x \cos\theta - A_y\sin\theta\,$

$A'_y = A_x \sin\theta + A_y\cos\theta\,$

las componentes del nuevo vector después de la rotación.

Las rotaciones en el plano pueden tratarse igualmente mediante números complejos, ya que e^iα es una rotación de ángulo a.

Teorema de rotación de Euler

En matemáticas, el teorema de rotación de Euler dice que cualquier rotación o conjunto de rotaciones sucesivas puede expresarse siempre como una rotación alrededor de una única dirección o eje de rotación principal. De este modo, toda rotación (o conjunto de rotaciones sucesivas) en el espacio tridimensional puede ser especificada a través del eje de rotación equivalente definido vectorialmente por tres parámetros y un cuarto parámetro representativo del ángulo rotado. Generalmente se denominan a estos cuatro parámetros grados de libertad de rotación.

Rotaciones en el espacio

Las rotaciones tridimensionales revisten especial interés por corresponderse con el espacio físico en que vivimos. En tres dimensiones conviene distinguir entre las rotaciones planas o rectangulares, que son aquellas en las que el vector rotado y el que determina el eje de giro forman un ángulo recto, y las cónicas, en las que el ángulo entre estos vectores no es recto. Las rotaciones planas son de tratamiento matemático más simple, pues se pueden reducir al caso bidimensional descrito más arriba, mientras que las cónicas son mucho más complejas y por lo general se tratan como una combinación de rotaciones planas (especialmente los ángulos de Euler y los parámetros de Euler-Rodrigues).

Las tres rotaciones planas de los ángulos de Euler. En la primera el eje es z, que apunta hacia arriba y gira los ejes x e y; en la segunda el eje es x, que apunta hacia el frente y que inclina el eje z, y en la última de nuevo el eje es z.

La expresión vectorial de las rotaciones cónicas es:

$\mathbf{r}' = ((1 -\cos \theta)\mathbf{uu}+ \cos \theta + \mathop{\mathrm{sen}} \theta \tilde{\mathbf{u}}) \cdot \mathbf{r}$

donde la expresión entre paréntesis funciona como operador y $\tilde{\mathbf{u}}= \mathbf{I}\times \mathbf{u}$ , de modo que $\tilde{\mathbf{u}}\cdot \mathbf{r}=\mathbf{u}\times\mathbf{r}$ . Hay ciertos casos especiales de este operador:

$\tilde{\mathbf{u}}$ es una rotación plana de (1/2)π rad. La aplicación sucesiva de este operador da $\tilde{\mathbf{u}}^2=-1$ , $\tilde{\mathbf{u}}^3=-\tilde{\mathbf{u}}$ , $\tilde{\mathbf{u}}^4=1$ , $\tilde{\mathbf{u}}^5=\tilde{\mathbf{u}}$ , etc., con un comportamiento parecido a la unidad imaginaria (i). Es un operador hemisimétrico y en coordenadas castesianas su matriz es:

$\begin{pmatrix} {0} & -u_z & u_y\\ u_z & {0} & -u_x\\ -u_y & u_x &{0}\\ \end{pmatrix}$

$\cos \theta + \mathop{\mathrm{sen}} \theta \tilde{\mathbf{u}}$ es una rotación plana de ángulo θ. Una notación alternativa es $\mathrm{e}^{\tilde{\mathbf{u}}\theta}$ . La forma matricial de este operador en los ejes cartesianos principales es particularmente sencilla; por ejemplo, para i es:

$\mathcal{R} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\mathrm{sen}\, \theta \\ 0 & \mathrm{sen}\, \theta & \cos \theta\end{bmatrix}$

$2\mathbf{uu}-1$ es una rotación cónica binaria (de π rad). Una rotación cónica arbitraria de ángulo θ se puede representar con dos rotaciones binarias, perpendiculares a $\mathbf{u}$ y que forman un ángulo (1/2)θ (Gibbs, p. 343-344); la manipulación de este par de rotaciones binarias (o, de modo equivalente, de dos reflexiones) se puede tomar como la base para la descripción mediante los parámetros de Euler-Rodrigues. Así, el segundo de estos ejes se obtiene mediante una rotación plana del primero con $\cos \frac{1}{2}\theta + \mathop{\mathrm{sen}} \frac{1}{2}\theta \tilde{\mathbf{u}}$ , que da los cuatro parámetros:

$\lambda =u_x \mathop{\mathrm{sen}} \theta/2\qquad \mu =u_y \mathop{\mathrm{sen}}\theta/2\qquad \nu=u_z \mathop{\mathrm{sen}}\theta/2\qquad \rho = \cos\theta/2$

Ángulos de Euler

Artículo principal: Ángulos de Euler

Mediante los ángulos de Euler se puede representar una rotación cualquiera con una sucesión de tres rotaciones planas alrededor de tres ejes ortogonales. No hay acuerdo sobre los tres ejes concretos y en la literatura científica aparecen diversos convenios; hay, en concreto, 12 posibilidades, pero lo más habitual es que se tomen zyz y zxz. A estos 12 convenios hay que añadir posibles variaciones en el signo, orientación relativa de ejes (horario o antihorario) y punto de vista (operación en vectores o transformación de coordenadas).

Los ángulos de Euler fueron el sistema más popular en los siglos XIX y XX para representar las rotaciones, pues permiten modelizar fácilmente varios sistemas mecánicos, como los trompos, los giroscopios, los barcos y los aviones. En el caso del trompo, los ejes se corresponden con la precesión, la nutación y la rotación. En los aviones se toman como ejes xyz, de modo que se correspondan con el alabeo (o balanceo en barcos), el cabeceo y la guiñada; este convenio específico de ejes se llama también ángulos de navegación o de Tait-Bryan.

Los ángulos de Euler presentan una singularidad cuando el ángulo del segundo giro es 0 o π, pues en tal caso el primer ángulo y el segundo pasan a quedar indefinidos, y solo está definida su suma, si el ángulo es 0. Con ello se pierde un grado de libertad, lo que en los dispositivos mecánicos que combinan varios ejes, como los giroscopios, puede conducir a un bloqueo del sistema, conocido como bloqueo de cardán (en inglés, gimbal lock). Matemáticamente, es posible evitar estas singularidades con sistemas de cuatro parámetros, como los parámetros de Euler-Rodrigues (o cuaterniones).

Parámetros de Euler-Rodrigues y cuaterniones

Los cuaterniones proporcionan un metodo para representar rotaciones que no presentan singularidades a costa de ser redundantes. Pueden introducirse axiomáticamente o derivarse a partir rotaciones vectoriales, es especial mediante la construcción de Rodrigues.

Históricamente, los cuatro parámetros que forman los cuaterniones fueron introducidos de modo independiente y con diferentes tratamientos matemáticos y geométricos por Gauss, Rodrigues y Hamilton, entre otros, aunque aparentemente Euler, a pesar del nombre, los desconocía. Rodrigues llegó a ellos mediante trigonometría esférica como una combinación de reflexiones; Hamilton, poco después, lo formuló de modo axiomático como una extensión de los números complejos. En mecánica cuántica también se llegó a ellos con las matrices de Pauli.

Concepto de rotación y revolución

Ejemplo de rotación.

Ejemplo de revolución.

El movimiento de la estructura de una noría corresponde a un movimiento de rotación. Por el contrario, las barquillas de la noria realizan un movimiento de traslación o revolución con trayectoria circular.

En astronomía es habitual distinguir entre el movimiento de rotación y el de revolución con los siguientes sentidos:

La rotación de un cuerpo alrededor de un eje (exterior o interior al cuerpo) corresponde a un movimiento en el que los distintos puntos del cuerpo presentan velocidades que son proporcionales a su distancia al eje. Los puntos del cuerpo situados sobre el eje (en el caso de que éste sea interior al cuerpo) permanecen en reposo.
- La orientación del cuerpo en el espacio cambia continuamente durante la traslación.
- Un ejemplo de rotación es el de la Tierra alrededor de su propio eje de rotación, con un periodo de rotación de un día sidéreo.
La revolución de una partícula o de un cuerpo extenso corresponde a un movimiento de traslación del cuerpo alrededor de otro.
- Un ejemplo de revolución es el de la Tierra alrededor del Sol, con un periodo de revolución de un año.

La distinción entre rotación y revolución esta asociada con la existente entre rotación y traslación de un cuerpo extenso. Si la velocidad de traslación es constante (v=cte), cada uno de los puntos del sólido recorrerá una trayectoria rectilínea con celeridad constante y todas esas trayectorias serán paralelas entre sí (movimiento de traslación uniforme). Pero, en general, la velocidad de traslación no tiene por que ser constante y la trayectoria puede ser curvilínea.

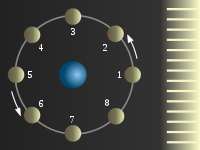
Las trayectorias recorridas por los distintos puntos del cuerpo pueden ser circunferencias, todas ellas del mismo radio (congruentes) aunque de distinto centro. Esta situación se presenta en una noria de feria de eje horizontal, como se muestra en la figura: la armadura de la noria gira en torno al eje (rotación), pero las barquillas suspendidas de dicha armadura, prescindiendo de pequeñas oscilaciones pendulares, experimentan una traslación con trayectorias circulares.

Movimiento rotatorio

Rotación infinitesimal

En una rotación en un ángulo infinitesimal δθ, se puede toma cos δθ ≈ 1 y sen δθ ≈ δθ, de modo que la expresión de la rotación plana pasa a ser:

$\mathbf{r}'=(1 + \delta\theta \tilde{\mathbf{u}}) \cdot \mathbf{r} = \mathbf{r} + \delta\theta \mathbf{u}\times\mathbf{r}$

Si se componen dos rotaciones infinitesimales y, por ello, se descartan los términos de orden superior al primero, se comprueba que poseen la propiedad conmutativa, que no tienen las rotaciones tridimensionales finitas.

Velocidad angular

Artículo principal: Cinemática del sólido rígido

La velocidad lineal v de una partícula se puede expresar a partir de la velocidad angular como:

$\mathbf{v} = \frac{d\mathbf{r}}{dt} = \boldsymbol\omega \times \mathbf{r}$

Mientras que la aceleración a es:

$\mathbf{a} = \boldsymbol{\alpha} \times \mathbf{r} + \boldsymbol\omega \times (\boldsymbol\omega \times \mathbf{r})$

Dinámica de rotación

La velocidad angular de rotación está relacionada con el momento angular. Para producir una variación en el momento angular es necesario actuar sobre el sistema con fuerzas que ejerzan un momento de fuerza. La relación entre el momento de las fuerzas que actúan sobre el sólido y la aceleración angular se conoce como momento de inercia (I) y representa la inercia o resistencia del sólido a alterar su movimiento de rotación.

La energía cinética de rotación se escribe:

$E_c = \frac{1}{2} \boldsymbol\omega \cdot (\mathbf{I} \boldsymbol\omega)$

siendo $\mathbb{I}$ el tensor momento de inercia.

La expresión del teorema del trabajo en movimientos de rotación se puede expresar así:

$\Delta E_c=\mathbf{M}\cdot\Delta\boldsymbol{\theta}$

de modo que, la variación de la energía cinética del sólido rígido es igual al producto escalar del momento de las fuerzas por el vector representativo del ángulo girado ( $Δθ$ ).

Teoría de grupos

Una rotación de un sexto de vuelta completa (2π/6) alrededor de un eje que atraviesa la pantalla deja igual la molécula de benceno, por lo que hay una simetría rotacional (entre otras).

En teoría de grupos, la rotación es una de las posibles transformaciones que se pueden aplicar a un sistema o una figura geométrica, que permiten determinar la simetría de redes cristalográficas, orbitales atómicos y moléculas, y por tanto parte de sus propiedades físico-químicas. Otras tranformaciones son la traslación, la reflexión y la inversión.

Rotaciones frente a traslaciones

En mecánica se demuestra que el movimiento del sólido rígido se puede descomponer en una rotación y una traslación. Ambas trasformaciones son isométricas, como corresponde al hecho de que el sólido es rígido, pero en la rotación, al contrario que en la traslación, hay al menos un punto fijo. El conjunto de estas transformaciones forma un grupo llamado grupo euclidiano, que se puede representar como:

$\begin{pmatrix} R & \mathbf{d}\\ \mathbf{0} & 1 \end{pmatrix}$

donde R es la matriz de rotación y d las componentes del vector de desplazamiento.

Rotaciones frente a reflexiones e inversiones

Estas tres transformaciones se llaman tranformaciones puntales pues dejan un punto fijo, y están estrechamente relacionadas. Así, dos reflexiones según dos planos equivalen a una rotación.

La composición de dos rotaciones tridimensionales es otra rotación, por lo que estas forman un grupo, llamado O(3) y que incluye las reflexiones. Las rotaciones propias son un subgrupo, llamado SO(3), pero no las rotaciones impropias, pues dos de ellas equivalen a una rotación propia.

Percepción de las rotaciones

Resultado.

Imagen original de la composición.

La imagen muestra un artificio para crear la ilusión de una rotación en 3D a partir de una imagen en 2D. Está formada por partes restringidas una detrás de otra, de modo que nuestro cerebro interpreta como una rotación de acuerdo a los datos que sobre el objeto (la cabeza) retiene nuestra memoria.

Véase también

Categorías:

Cinemática
Simetría euclidiana
Transformaciones geométricas

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Sinónimos:

giro, vuelta, rodeo, viraje, revolución, curva, desvío

Mira otros diccionarios:

rotación — f. fís. Movimiento de un cuerpo alrededor de su eje. Medical Dictionary. 2011. rotación 1. giro alrededor de un … Diccionario médico
rotación — sustantivo femenino 1. Área: astronomía, física Acción y resultado de rodar o dar vueltas un cuerpo sobre su eje: la rotación de la Tierra. Locuciones 1. rotación de cultivos Área: agricultura … Diccionario Salamanca de la Lengua Española
rotación — (Del lat. rotatĭo, ōnis). f. Acción y efecto de rotar1. rotación de cultivos. f. Variedad de siembras alternativas o simultáneas, para evitar que el terreno se agote en la exclusiva alimentación de una sola especie vegetal. ☛ V. capital de… … Diccionario de la lengua española
rotación — de personal … Diccionario de Economía Alkona
rotación — de personal … Diccionario de Economía
Rotación — ► sustantivo femenino 1 Acción y resultado de rotar o girar un cuerpo sobre su eje, en especial se aplica al movimiento que realizan los cuerpos celestes: ■ la Tierra tarda veinticuatro horas en realizar el movimiento de rotación. SINÓNIMO… … Enciclopedia Universal
rotación — s f 1 Acto de rotar alguna cosa o una persona: la rotación de la Luna, la rotación de la Tierra 2 Cambio alternativo o periódico del lugar o posición que ocupan los elementos de un conjunto, o de un elemento por otro: rotación de puestos,… … Español en México
rotación — {{＃}}{{LM R34597}}{{〓}} {{SynR35457}} {{［}}rotación{{］}} ‹ro·ta·ción› {{《}}▍ s.f.{{》}} {{＜}}1{{＞}} Movimiento de un cuerpo alrededor de su eje: • La rotación de la Tierra dura aproximadamente veinticuatro horas.{{○}} {{＜}}2{{＞}} Alternancia de… … Diccionario de uso del español actual con sinónimos y antónimos
rotación — (f) (Intermedio) giro de un cuerpo alrededor de un eje Ejemplos: La rotación de las agujas del reloj sirve para medir el tiempo. Las rotaciones del motor generan potencia eléctrica. Sinónimos: vuelta, revolución, giro, curva, desvío, rodeo,… … Español Extremo Basic and Intermediate
Rotación trienal — Saltar a navegación, búsqueda La Rotación Trienal era una técnica agraria básica del siglo XIII, que era un sistema de cultivo propio de la Europa Atlántica. Se basa en la sucesión en el campo de cultivo de un cereal de invierno el primer año, un … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Rotación

Contenido