Gráfica de una función

En matemáticas, la gráfica de una función:

$\begin{array}{rccl} f: & X & \longrightarrow & Y \\ & x & \longmapsto & y= f(x) \end{array}$

es la visualización de la correspondencia entre los elementos del conjunto dominio y los del conjunto imagen mediante su representación iconográfica. También puede definirse como el conjunto formado por todos los pares ordenados (x, f(x)) de la función f; es decir, como un subconjunto del producto cartesiano X×Y.

Las únicas funciones que se pueden visualizar de forma completa son las de una sola variable, representables como un sistema de coordenadas cartesianas, donde cada abscisa representa un valor de la variable del dominio y cada ordenada representa el valor correspondiente del conjunto imagen. Si la función es continua, entonces la gráfica formará una curva.

En el caso de funciones de dos variables es posible visualizarlas de forma unívoca mediante una proyección geométrica, pero a partir de tres variables tan solo es posible visualizar cortes de la función para los que los valores de todas las variables excepto dos permanezcan constantes.

El concepto de gráfica de una función se generaliza a la gráfica de una relación. Notar que si bien cada función tiene una única representación gráfica, pueden existir varias funciones que tengan la misma, pero con dominios y codominios diferentes.

Contenido

1 Dominio de definición
2 Puntos de discontinuidad
- 2.1 Galería de discontinuidades
3 Ejemplos
4 Método para representar la gráfica de una función de una variable
5 Véase también
- 5.1 Herramientas para dibujar la gráfica de una función
6 Enlaces externos

Dominio de definición

El Dominio de definición D de una función es el subconjunto de X que tienen imagen en Y:

$D \subset X \; | \quad \forall x \in D: \; \exists y \in Y \quad \land \quad y= f(x)$

Sin pérdida de la generalidad, consideramos, tanto el conjunto X como Y sea el de los números reales R, siendo X un intervalo o la unión de varios intervalos, podemos diferenciándose los siguientes casos:

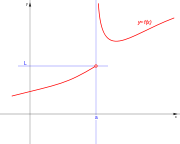
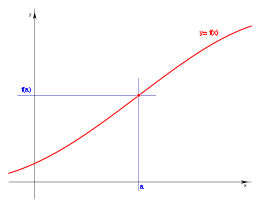
El dominio un intervalo abierto: (a,b). Se puede expresar:

$D = \big \{ x \in \R \quad \land \quad a < x < b \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real y a sea menor que x y x menor de b, tal que existe y número real é y= f(x).

La forma de representar el intervalo abierto, da lugar a la expresión:

$D = \big \{ x \in \R \quad \land \quad x \in (a, b) \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real en el intervalo abierto (a,b) , tal que existe y número real é y= f(x).

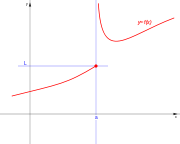
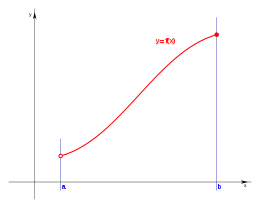
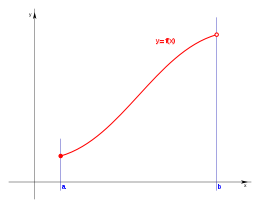
Si el dominio un intervalo semiabierto: (a,b]. Tenemos la expresión:

$D = \big \{ x \in \R \quad \land \quad a < x \leq b \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real y a sea menor o igual que x y x menor de b, tal que existe y número real é y= f(x).

Tomando la forma de representar un intervalo semiabierto, tenemos la expresión:

$D = \big \{ x \in \R \quad \land \quad x \in (a, b] \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real en el intervalo semiabierto [a,b) , tal que existe y número real é y= f(x).

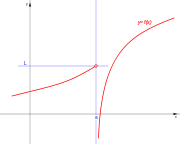
Si el dominio es el intervalo semiabierto: [a,b). Tenemos la expresión:

$D = \big \{ x \in \R \quad \land \quad a \leq x < b \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real y a sea menor que x y x menor o igual que b, tal que existe y número real é y= f(x).

Tomando la forma de representar un intervalo semiabierto, tenemos la expresión:

$D = \big \{ x \in \R \quad \land \quad x \in [a, b) \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real en el intervalo semiabierto [a,b) , tal que existe y número real é y= f(x).

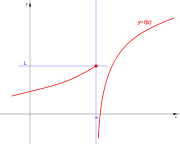
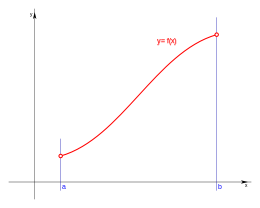
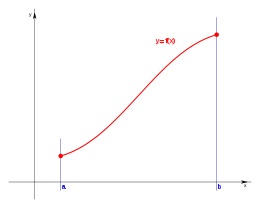
Si el dominio un intervalo cerrado: [a,b] la expresión resultante es:

$D = \big \{ x \in \R \quad \land \quad a \leq x \leq b \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real y a sea menor o igual que x y x menor o igual que b, tal que existe y número real é y= f(x).

Tomando la forma de representar un intervalo cerrado, tenemos que:

$D = \big \{ x \in \R \quad \land \quad x \in [a, b] \; | \; \exists y \in \R \quad \land \quad y= f(x) \big \}$

El dominio D es el conjunto de elementos x, número real en el intervalo cerrado [a,b] , tal que existe y número real é y= f(x).

En estos ejemplos hemos podido ver, las distintas formas de representar los distintos tipos de intervalos, tanto abiertos semiabiertos o cerrados, en una expresión o en una gráfica.

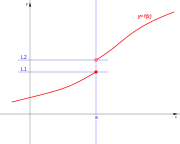
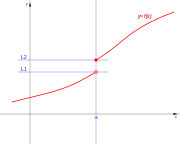
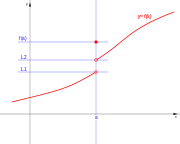
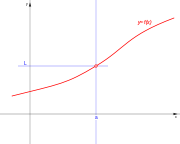
Puntos de discontinuidad

Artículo principal: Clasificación de discontinuidades

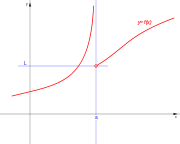
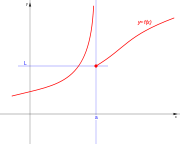
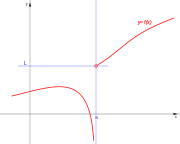
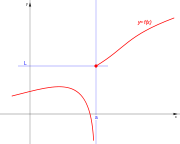
En los puntos extremos de cada intervalo de definición de la función, o en los puntos intermedios de los intervalos de existencia, que presenten discuntinuidad, se presenta un punto de discontinuidad, que puede ser de alguno de estos tipos:

$Discontinuidad { \color{Red} \left \{ \begin{array}{l} Evitable \\ Esencial { \color{PineGreen} \left \{ \begin{array}{l} De \; primera \; especie { \color{Blue} \left \{ \begin{array}{l} De \; salto \; finito \\ De \; salto \; infinito \\ Asint \acute{o} tica \end{array} \right . }\\ \\ De \; segunda \; especie \end{array} \right . } \\ \end{array} \right . }$

Galería de discontinuidades


$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = \infty \\ \\ \nexists \; \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = -\infty \\ \\ \nexists \; \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L \\ \\ \nexists \; \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L \\ \\ \nexists \; \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) \\ \\ f(a) = L \end{array} \right .$
De segunda especie.	De segunda especie.	De segunda especie.	De segunda especie.


$\left \{ \begin{array}{l} \nexists \; \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = \infty \end{array} \right .$	$\left \{ \begin{array}{l} \nexists \; \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = -\infty \end{array} \right .$	$\left \{ \begin{array}{l} \nexists \; \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = L \end{array} \right .$	$\left \{ \begin{array}{l} \nexists \; \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = L \\ \\ f(a) = L \end{array} \right .$
De segunda especie.	De segunda especie.	De segunda especie.	De segunda especie.


$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = \infty \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = \infty \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = -\infty \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = \infty \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = \infty \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = -\infty \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = -\infty \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = -\infty \end{array} \right .$
Asintótica.	Asintótica.	Asintótica.	Asintótica.


$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = \infty \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = \infty \\ \\ f(a) = L \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = -\infty \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = -\infty \\ \\ f(a) = L \end{array} \right .$
De salto infinito.	De salto infinito.	De salto infinito.	De salto infinito.


$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = \infty \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = L \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = \infty \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = L \\ \\ f(a) = L \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = -\infty \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = L \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = -\infty \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = L \\ \\ f(a) = L \end{array} \right .$
De salto infinito.	De salto infinito.	De salto infinito.	De salto infinito.


$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L1 \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = L2 \\ \\ L1 \ne L2 \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L1 \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = L2 \\ \\ L1 \ne L2 \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L1 \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = L2 \\ \\ L1 \ne L2 \end{array} \right .$	$\left \{ \begin{array}{l} \underset{x \to {a}^{-}}{L \acute{\imath}m} \; f(x) = L \\ \\ \underset{x \to {a}^{+}}{L \acute{\imath}m} \; f(x) = L \\ \\ \nexists \; f(a) \end{array} \right .$
De salto finito.	De salto finito.	De salto finito.	Evitable

Ejemplos

Gráfica de la función x³-9x.

La gráfica de la función

$f(x)=\left\{\begin{matrix} a, & \mbox{si }x=1 \\ b, & \mbox{si }x=2 \\ c, & \mbox{si }x=3. \end{matrix}\right.$

es {(1,a), (2,b), (3,c)}.

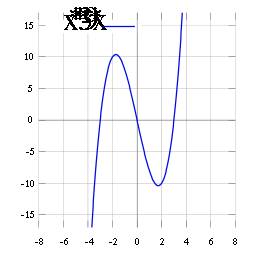
La gráfica del polinomio cúbico en la recta real

$f(x)={{x^3}-9x} \!\$

es {(x,x³-9x) : donde x es un número real}. Si el conjunto se representa en un plano cartesiano, el resultado es como el de la imagen.

Método para representar la gráfica de una función de una variable

Artículo principal: Representación gráfica de una función

Para dibujar, construir o representar la gráfica de una función f se pueden seguir los pasos siguientes:

Buscar el dominio de la función, Dom f(x)
Se detectan aquellos valores x reales en que f sea discontinua, es decir, aquellos que no estén definidos en el dominio, y se procede a estudiar los límites cuando x tiene a x por la izquierda y por la derecha. De este modo, si x es un punto aislado y no un intervalo, se puede deducir hacia dónde tiende la función cuando pasa cerca del punto x.
Buscar los límites cuando x tiende a infinito o menos infinito, para averiguar cuándo en el eje de abscisas se tiende al resultado del límite.
Estudio de la monotonía. Calculando la primera derivada f'(x) e igualándola a cero, se obtienen los posibles candidatos a extremos de la función. Luego se procede a determinar si f(x) es creciente o decreciente entre dos puntos extremos.
Se estudia la curvatura de f, igualando a cero esta vez la segunda derivada f(x), obteniéndose los posibles puntos de inflexión. Se estudia el signo en la f(x) en los intervalos, y así, sea x uno de estos puntos:

Si f(x) es negativa, entonces f(x) es cóncava

Si f(x) es positiva, entonces f(x) es convexa.

Véase también

Herramientas para dibujar la gráfica de una función

Enlaces externos

Algunosapplets Java para funciones reales
Weisstein, Eric W. "Function Graph." From MathWorld--A Wolfram Web Resource.

Categoría:

Funciones

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

Representación gráfica de una función — Saltar a navegación, búsqueda En matemáticas la representación gráfica es una ayuda para el estudio de una función. Una función con una variable dependiente y otra independiente se puede representar gráficamente en un eje de ordenadas y abscisas… … Wikipedia Español
Paridad de una función — Saltar a navegación, búsqueda En matemáticas, se puede clasificar a las funciones según su paridad. Las funciones pueden ser pares, impares o no tener paridad. Aquellas funciones que poseen paridad satisfacen una serie de relaciones particulares… … Wikipedia Español
Raíz de una función — Saltar a navegación, búsqueda Si busca la raíz enésima de un número, vea Función raíz. En matemática, se conoce como raíz (o cero) de una función (definida sobre un cierto cuerpo algebraico) f (x) a todo elemento x perteneciente al dominio de… … Wikipedia Español
Función par — En matemáticas, una función par es cualquier función que satisface la relación para todo valor admisible de x. La gráfica de dicha función es simétrica respecto al eje y. Contenido 1 Definición formal … Wikipedia Español
Función monótona — En matemáticas, una función entre conjuntos ordenados se dice monótona (o isótona) si conserva el orden dado. Las funciones de tal clase surgieron primeramente en cálculo, y fueron luego generalizadas al entorno más abstracto de la teoría del… … Wikipedia Español
Función de probabilidad — Para otros usos de este término, véase medida de probabilidad. En teoría de la probabilidad, una función de probabilidad (también denominada función de masa de probabilidad) es una función que asocia a cada punto de su espacio muestral X la… … Wikipedia Español
Función real — Una función real es una función matemática cuyo dominio y codominio están contenidos en , es decir, es una función: En general se trata de funciones continuas, o bien discontinuas cuando están representadas por tramos, a diferencia de las… … Wikipedia Español
Función error — Gráfica de la función error. En matemáticas, la función error (también conocida como función error de Gauss) es una función especial (no elemental) que se utiliza en el campo de la probabilidad, la estadística y las ecuaciones diferenciales… … Wikipedia Español
Función constante — En matemática se llama función constante a aquella función matemática que toma el mismo valor para cualquier valor de la variable. Se la representa de la forma:[1] donde c es la constante. Conten … Wikipedia Español
Función polinómica de grado 0 — Saltar a navegación, búsqueda Se llama función polinómica de grado cero o función constante a la que no depende de ninguna variable, y la podemos representar como una función matemática de la forma: donde a es la constante. Como se puede ver es… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Gráfica de una función

Contenido

Dominio de definición

Puntos de discontinuidad

Galería de discontinuidades

Ejemplos

Método para representar la gráfica de una función de una variable

Véase también

Herramientas para dibujar la gráfica de una función

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Gráfica de una función

Contenido

Dominio de definición

Puntos de discontinuidad

Galería de discontinuidades

Ejemplos

Método para representar la gráfica de una función de una variable

Véase también

Herramientas para dibujar la gráfica de una función

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo