Números de Catalan

Números de Catalan
Números de Catalan
n C_n \,
0 1
1 1
2 2
3 5
4 14
5 42
6 132
7 429
8 1.430
9 4.862
10 16.796
11 58.786
12 208.012
13 742.900
14 2.674.440
15 9.694.845
16 35.357.670
17 129.644.790
18 477.638.700
19 1.767.263.190
20 6.564.120.420
21 24.466.267.020
22 91.482.563.640
23 343.059.613.650
24 1.289.904.147.324
25 4.861.946.401.452

En combinatoria, los números de Catalan forman una secuencia de números naturales que aparece en varios problemas de conteo que habitualmente son recursivos. Obtienen su nombre del matemático belga Eugène Charles Catalan (1814–1894).

El n-ésimo número de Catalan se obtiene, aplicando coeficientes binomiales, a partir de la siguiente fórmula:

C_n = \frac{1}{n+1}{2n\choose n} = \frac{(2n)!}{(n+1)!\,n!} \qquad\mbox{ con }n\ge 0.

Propiedades

Una expresión alternativa para Cn es

C_n = {2n\choose n} - {2n\choose n-1} \quad\mbox{ con }n\ge 1.

Esta otra expresión muestra que Cn es un número natural, lo cual no resulta obvio a priori mirando la primera fórmula dada.

Los números de Catalan satisfacen la siguiente relación de recurrencia:

C_0 = 1 \quad \mbox{y} \quad C_{n+1}=\sum_{i=0}^{n}C_i\,C_{n-i}\quad\mbox{con }n\ge 0.

Y también satisfacen:

C_0 = 1 \quad \mbox{y} \quad C_{n+1}=\frac{2(2n+1)}{n+2}C_n,

que puede ser una forma más eficiente de calcularlos.

La expresión en forma de recursión, seria:

C_{n} = \begin{cases} \mbox{si }n=0 & \Rightarrow 1 \\ \mbox{si }n>0 & \Rightarrow \cfrac{2(2n-1)}{n+1} \, C_{n-1} \end{cases}

Asintóticamente, los números de Catalan crecen como:

C_n \sim \frac{4^n}{n^{3/2}\sqrt{\pi}}

considerando que el cociente entre el n-ésimo número de Catalan y la expresión de la derecha tiende hacia 1 cuando n → ∞ (esto puede probarse usando la fórmula de Stirling).

Aplicaciones en combinatoria

Existen múltiples problemas de combinatoria cuya solución la dan los números de Catalan. El libro Enumerative Combinatorics: Volume 2 de Richard P. Stanley contiene un conjunto de ejercicios que describen 66 interpretaciones distintas de los números de Catalan. Aquí se muestran algunos ejemplos, con ilustraciones para el caso C3 = 5.

  • Cn es el número de palabras de Dyck de longitud 2n. Una palabra de Dyck es una cadena de caracteres que consiste en n X's y n Y's de forma que no haya ningún segmento inicial que tenga más Y's que X's. Por ejemplo, lo siguiente son las palabras de Dyck de longitud 6:
XXXYYY     XYXXYY     XYXYXY     XXYYXY     XXYXYY
  • Reinterpretando el símbolo X como un paréntesis abierto y la Y como un paréntesis cerrado, Cn cuenta el número de expresiones que contienen n pares de paréntesis correctamente colocados:
((()))     ()(())     ()()()     (())()     (()())
  • Cn es el número de formas distintas de agrupar n + 1 factores mediante paréntesis (o el número de formas de asociar n aplicaciones de un operador binario). Para n = 3 por ejemplo, tenemos las siguientes cinco formas distintas de agrupar los cuatro factores:
((ab)c)d \quad (a(bc))d \quad(ab)(cd) \quad a((bc)d) \quad a(b(cd))
  • Las aplicaciones sucesivas de un operador binario pueden representarse con un árbol binario. En este caso, Cn es el número de árboles binarios de n + 1 hojas, en los que cada nodo tiene cero o dos hijos:
Catalan 4 leaves binary tree example.svg
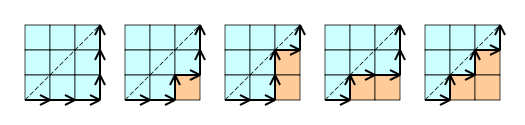
  • Cn es el número de caminos monótonos que se pueden trazar a través de las líneas de una malla de n × n celdas cuadradas, de forma que nunca se cruce la diagonal. Un camino monótono es aquél que empieza en la esquina inferior izquierda y termina en la esquina superior derecha, y consiste únicamente en tramos que apuntan hacia arriba o hacia la derecha. El recuento de estos caminos es equivalente a contar palabras de Dyck: X significa "moverse a la derecha" e Y significa "moverse hacia arriba". Los siguientes diagramas muestran el caso n = 3:
Catalan number 3x3 grid example.svg
  • Cn es el número de formas distintas de cortar un polígono convexo de n + 2 lados en triángulos conectando vértices con líneas rectas sin que ninguna se corte. La siguiente figura ilustra el caso de los polígonos de 5 lados, cuando n = 3:
Catalan number polygon cut into triangles example.svg

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Números de Catalan — En combinatoria los números de Catalan forman una secuencia de números naturales que aparece en varios problemas de conteo que habitualmente son recursivos. Obtienen su nombre del matemático belga Eugène Charles Catalan (1814–1894). El nésimo… …   Enciclopedia Universal

  • Cálculo de los números de Catalan — Saltar a navegación, búsqueda Los números de catalán obtienen su nombre del matemático Eugène Charles Catalán (1814–1894) de origen belga. Se utilizan en combinatoria y estos son una secuencia de números naturales que aparecen en varios problemas …   Wikipedia Español

  • Catalán — Saltar a navegación, búsqueda Catalán puede referirse a: algo relativo a Cataluña; el idioma catalán. el pueblo catalán. En geografía: Catalán (Estado Nueva Esparta), Venezuela. Arroyo Catalán, arroyo de Uruguay. En astronomía: Catalán, un cráter …   Wikipedia Español

  • Eugène Charles Catalan — Saltar a navegación, búsqueda Eugène Charles Catalan Eugène Charles Catalan (30 de mayo de 1814 14 de febrero de 1894) fue un matemático belga que trabajó en la teoría de números …   Wikipedia Español

  • Conjetura de Catalan — La conjetura de Catalan (también conocida como teorema de Mihăilescu) es un teorema de teoría de números propuesto por el matemático Eugène Charles Catalan en 1884 y demostrado por primera vez por Preda Mihăilescu en abril de 2002. Para entender… …   Wikipedia Español

  • Conjetura de Catalan — La conjetura de Catalan es una conjetura de la teoría de números propuesta por el matemático Eugène Charles Catalan. Para entender esta conjetura, nótese que 2³ = 8 y 3² = 9 son dos números que son potencias consecutivas de números naturales. La… …   Enciclopedia Universal

  • Conjetura de Fermat–Catalan — En teoría de números, la conjetura de Fermat–Catalan combina ideas del último teorema de Fermat y de la conjetura de Catalan, de ahí el nombre. La conjetura postula que la ecuación (1) tiene un número finito de soluciones (a,b,c,m,n,k); aquí a, b …   Wikipedia Español

  • Constante de Catalan — La constante de Catalan debe su nombre al matemático belga Eugène Charles Catalan y aparece en el contexto de las integrales elípticas y su valor resulta ser un número irracional igual a la suma alternada de los inversos de los cuadrados de los… …   Wikipedia Español

  • Eugène Charles Catalan — (1814 1894) fue un matemático belga que trabajó en teoría de números. Él introdujo el número de Catalan para resolver problemas de combinación. Siendo profesor en la Escuela Politécnica de París, describió la famosa conjetura de Catalan, que fue… …   Enciclopedia Universal

  • Número doble de Mersenne — En matemáticas, un número doble de Mersenne es un número de Mersenne de la forma donde el exponente 2n − 1 es a su vez el número de Mersenne Mn, con n natural. Números dobles de Mersenne primos A menudo se consideran solamente los números dobles… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”