Una red libre de escala es un tipo específico de red compleja. En una red libre de escala, algunos nodos están altamente conectados, es decir, poseen un gran número de enlaces a otros nodos, aunque el grado de conexión de casi todos los nodos es bastante bajo.

Historia

Lászlo Barabási y sus colaboradores de la Universidad de Notre Dame en Indiana (EE. UU.) hicieron un mapa de la Web en 1999. Para su sorpresa, la web no presentaba una distribución del grado de conectividad usual. En lugar de esto, algunos pocos nodos, a los que llamaron "hubs", estaban mucho más conectados que el resto. Al mismo tiempo, una observación similar sobre internet fue obtenida por los hermanos Faloutsos (1999). Y más tarde Broder et al. (2000) corroboraron estos hallazgos con un mapa de la Web más completo. (véase tmabién Modelo Barabási–Albert).^[1]

En general, encontraron que la probabilidad p(k) de que un nodo de la red estuviera conectado con k nodos era proporcional a k ^{− γ}, es decir, sigue una ley de potencias. El exponente γ no es universal, sino que depende del tipo específico de red. Para la mayor parte de los sistemas se encontró que dicho parámetro se encontraba en el rango 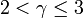. Cuando 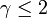, la varianza de la distribución del número de enlaces por nodo es infinita.

Ejemplos

Además del ejemplo de las redes de páginas Web, existen muchas otras redes libres de escala:

• La red de amistades entre personas. Esto también se puede extender a las redes de llamadas telefónicas, de envíos postales y de correo electrónico, por ejemplo.
• La red de contactos sexuales entre personas. Hay unas pocas personas que tienen muchas parejas a lo largo de su vida, mientras que la mayoría de las personas tiene unas pocas parejas.
• Las redes del crimen organizado, en los cuales unos cuantos "peces gordos" ordenan la actuación de muchos "peces chicos".
• La red de distribución eléctrica, en que existen estaciones enormes que abastecen a zonas enormes, y al mismo tiempo una miríada de transformadores pequeños.^[2]
• Las redes de comercio internacional, dado que los países desarrollados, que son la minoría, concentran la mayor cantidad de intercambio de bienes, mientras que en los países no desarrollados, que son la mayoría, el intercambio comercial es relativamente menor. Esto se aplica también a las redes de comercio entre empresas dentro de cada país.
• Las redes de citaciones bibliográficas incluyen unos pocos libros o escritos muy citados, mientras que la mayoría de los libros reciben pocas o incluso ninguna citación.
• Las redes de neuronas en los organismos dotados de sistema nervioso, lo que significa que permanentemente usamos mucho una fracción de las neuronas, mientras que la mayoría de las neuronas las ocupamos muy poco.
• Las redes de interacción de proteínas en el metabolismo celular, con unas pocas proteínas que aparecen en la mayoría de las reacciones, mientras que la mayoría de las proteínas aparecen sólo en situaciones muy específicas.
• Las redes de caminos, pues la mayoría de los caminos llegan a unas pocas ciudades muy grandes, mientras que de la mayoría de ciudades pequeñas salen unos pocos caminos. Lo mismo es válido para las rutas marítimas y los puertos, las rutas aéreas y los aeropuertos.

Véase también

• Modelo Barabási–Albert

Bibliografía

• Albert, R., Jeong, H. & Barabasi, A. L. Diameter of the world-wide web. Nature 401, 130-131 (1999).
• Faloutsos, M., Faloutsos, P. & Faloutsos, C. On power-law relationship of the internet topology. Comp Comm Rev 29, 251-262 (1999).
• Broder, A. et al. Graph structure in the Web. Comput Networks 33, 309-320 (2000).

Referencias

Referencias Externas

• Redes libres de escala - explicación con diagramas en Tejedores del Web.