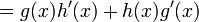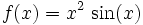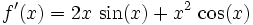- Regla del producto
-
Regla del producto
En análisis matemático, la regla del producto o regla de Leibniz para la derivación de un producto, gobierna la derivación del producto de funciones derivables.
Puede declararse informalmente como "la derivada de la primera por la segunda sin derivar más la primera sin derivar por la derivada de la segunda" o matemáticamente:
Obviamente al resolverse como una suma de productos, el orden no importa, lo importante es que no se confunda f(x), g(x), f'(x) y g'(x).
Prueba de la regla del producto
Se puede derivar la regla usando las características del límite y la definición de la derivada como el límite del cociente de la diferencia.
Se comienza con:
suponiendo que g y h son diferenciables en la variable x. Entonces
Como
se tiene
Como h es continua en x, se tiene
y por la definición de la derivada, y la diferenciabilidad de h y g en x, se tiene también
![\left[\lim_{\Delta x \to 0} \frac{(h(x + \Delta x) - h(x))}{\Delta x}\right] = h'(x)](/pictures/eswiki/49/1b9af7dad4cde09483d53caf999a9b21.png) y
y ![\left[\lim_{\Delta x \to 0} \frac{(g(x + \Delta x) - g(x))}{\Delta x}\right] = g'(x)](/pictures/eswiki/97/abd5df2379d75a584fa4199a0439a85c.png)
Así, se justifica la descomposición de los productos dentro del límite, y reorganizando todo se tiene
lo cual termina la prueba.
Ejemplo
Suponiendo que se quiere derivar:
Usando la regla del producto, se obtiene la derivada:
- ya que la derivada de
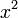 es
es 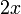
- y la derivada de
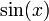 es
es 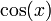 .
.
Categoría: Análisis matemático
Wikimedia foundation. 2010.

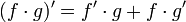
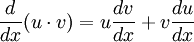 (
(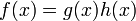
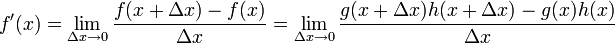
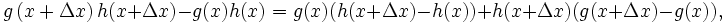
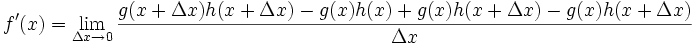
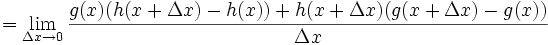
![= \lim_{\Delta x \to 0} \left[g(x)\left(\frac{(h(x + \Delta x) - h(x))}{\Delta x}\right) + h(x + \Delta x)\left(\frac{(g(x + \Delta x) - g(x))}{\Delta x}\right)\right]](/pictures/eswiki/100/dbcff10bb18f4714b053d5cc6ff4af05.png)
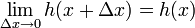
![f'(x) = \lim_{\Delta x \to 0} \left[g(x)\left(\frac{(h(x + \Delta x) - h(x))}{\Delta x}\right) + h(x + \Delta x)\left(\frac{(g(x + \Delta x) - g(x))}{\Delta x}\right)\right]](/pictures/eswiki/97/afd3431f78cb1ab0bfbc18a041ee33fb.png)
![= \left[\lim_{\Delta x \to 0} g(x)\right]\left[\lim_{\Delta x \to 0} \frac{(h(x + \Delta x) - h(x))}{\Delta x}\right] + \left[\lim_{\Delta x \to 0} h(x + \Delta x)\right]\left[\lim_{\Delta x \to 0}\frac{(g(x + \Delta x) - g(x))}{\Delta x}\right]](/pictures/eswiki/52/437921f2bf9c04ad12b8b25b2af8affe.png)