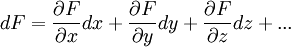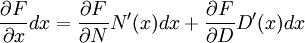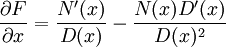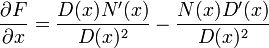- Regla del cociente
-
Regla del cociente
En cálculo, la regla del cociente es un método de encontrar la derivada de una función que es el cociente de dos otras funciones para las cuales existe la derivada.
La función a derivar, f(x), puede escribirse como
y h(x) ≠ 0, entonces la regla afirma que la derivada de g(x) / h(x) es igual a:
O de forma más precisa, para toda x que pertenece a algún conjunto abierto que contiene al número a, con h(a) ≠ 0; y, tal que existen g'(a) y h'(a); entonces, f'(a) también existe:
Contenido
Ejemplo
La derivada de (4x − 2) / (x2 + 1) es:
El de abajo por la derivada del de arriba menos el de arriba por la derivada del de abajo, sobre el de abajo al cuadrado.
En el ejemplo de arriba, se ha escogido:
- g(x) = 4x − 2
- h(x) = x2 + 1
De forma análoga, la derivada de sin(x) / x2 (cuando x ≠ 0) es:
Para más información en lo referente a las derivadas de las funciones trigonométricas, véase: derivada.
Otro ejemplo es:
donde g(x) = 2x2 y h(x) = x3, g'(x) = 4x y h'(x) = 3x2.
La derivada de f(x) se determina tal como sigue:
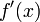
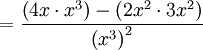
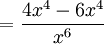
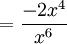
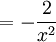
Demostraciones
A partir de la definición de derivada
- Suponiendo que f(x) = g(x) / h(x)
- donde h(x)≠ 0 y g y h son derivables.
A partir de la regla del producto
- Suponiend
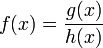
El resto consiste al aplicar las reglas del álgebra para hacer que f'(x) sea el único término del miembro izquierdo de la ecuación y para eliminar f(x) del miembro derecho de la ecuación.De forma alternativa, se puede aplicar la regla del producto directamente, sin tener que usar la sustitución:
Y acto seguido aplicar la regla de la cadena para derivar h(x) − 1:
A partir de la regla de la cadena
Se considera la identidad
Entonces
Lleva a
Operando se obtiene
Para acabar, se saca común denominador y queda el resultado esperado
Utilizando diferenciales totales
Una demostración incluso más elegante es consecuencia de la ley referente a los diferenciales totales, que dice que el diferencial total,
de cualquier función en cualquier conjunto de cantidades se puede descomponer de la siguiente forma, sin importar qué variables independientes haya en la función (es decir, no importa qué variables se tomen ya que no pueden expresarse como funciones de otras variables). Eso quiere decir que, si N y D son las dos funciones de una variable independiente x, y F = N(x) / D(x), entonces ha de ser verdad simultáneamente que
- (*)
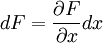
Y que
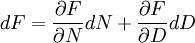 .
.
Pero sabiendo que dN = N'(x)dx y dD = D'(x)dx.
Sustituyendo y haciendo estos diferenciales totales iguales a un tercero (dado que representan límites que se pueden manipular), se obtiene la ecuación
La cual requiere que
- (#)
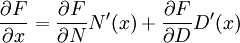 .
.
Calculando las parciales de la derecha:
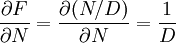 ;
;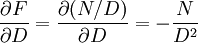 .
.
Si se sustituyen dentro de (#),
La cual da la regla del cociente, dado que, para (*),
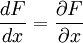 .
.
Esta demostración es una forma más sistemática de demostrar el teorema en términos de límites, y por lo tanto, es equivalente a la primera demostración - e incluso se reduce a ella si se hacen las sustituciones adecuadas en los lugares adecuados.
Véase también
Categoría: Cálculo
Wikimedia foundation. 2010.

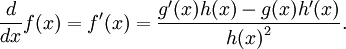
![f'(a)=\frac{g'(a)h(a) - g(a)h'(a)}{[h(a)]^2}.](/pictures/eswiki/99/c1fb89063c9c2285cffa29f34ca44490.png)
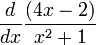
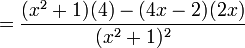
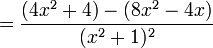
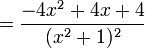
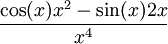
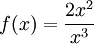
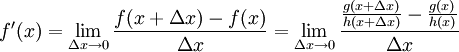
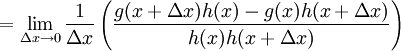
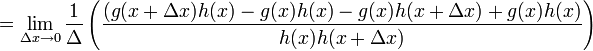
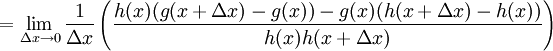
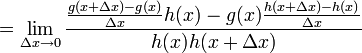
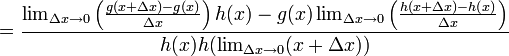
![= \frac{g'(x)h(x) - g(x)h'(x)}{[h(x)]^2}](/pictures/eswiki/55/79455cf2bc5ba292947ea4e5fa92ab3f.png)
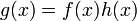
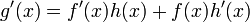
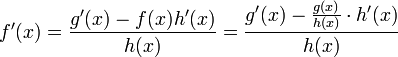
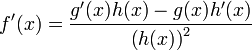
![f(x) = \frac{g(x)}{h(x)} = g(x) [h(x)]^{-1}](/pictures/eswiki/49/1286ec209ca9e0df9681e74282f77fcf.png)
![f'(x) = g'(x) [h(x)]^{-1} + g(x) (-1) [h(x)]^{-2} h'(x) = \frac{g'(x) h(x) - g(x) h'(x)}{[h(x)]^2}](/pictures/eswiki/51/35f8950abf04f2a17bc0bd4f524390c0.png)
![\frac{u}{v}\; =\; \frac{1}{4}\left[ \left( u+\frac{1}{v} \right)^{2}-\; \left( u-\frac{1}{v} \right)^{2} \right]](/pictures/eswiki/54/60bc449c145864d6aff210c363124d93.png)
![\frac{d\left( \frac{u}{v} \right)}{dx}\; =\; \frac{d}{dx}\frac{1}{4}\left[ \left( u+\frac{1}{v} \right)^{2}-\; \left( u-\frac{1}{v} \right)^{2} \right]](/pictures/eswiki/51/3cb39a303706e6cc43740c40ab8617e0.png)
![\frac{d\left( \frac{u}{v} \right)}{dx}\; =\; \frac{1}{4}\left[ 2\left( u+\frac{1}{v} \right)\left( \frac{du}{dx}-\frac{dv}{v^{2}dx} \right)-\; 2\left( u-\frac{1}{v} \right)\left( \frac{du}{dx}+\frac{dv}{v^{2}dx} \right) \right]](/pictures/eswiki/101/ec5d0c8ab79b13a3b4dc0fbb63918567.png)
![\frac{d\left( \frac{u}{v} \right)}{dx}\; =\; \frac{1}{4}\left[ \frac{4}{v}\frac{du}{dx}-\frac{4u}{v^{2}}\frac{dv}{dx} \right]](/pictures/eswiki/53/5439cee6a06381bcc7791e123632cc92.png)
![\frac{d\left( \frac{u}{v} \right)}{dx}\; =\; \frac{\left[ v\frac{du}{dx}-u\frac{dv}{dx} \right]}{v^{2}}](/pictures/eswiki/100/dbbafcd15e3b438d569c42f5639cb51d.png)