Regla del producto (Combinatoria)

Regla del producto (Combinatoria)

Regla del producto (Combinatoria)

En combinatoria, la regla del producto es una regla de recuento básica. Enunciada de manera simple, es la idea de que si algo puede hacerse de a formas y otra cosa puede hacerse de b formas, entonces hay a · b formas de hacer ambas cosas. Así, elegir un elemento de {A, B, C} y otro de {X, Y} es elegir un elemento de {AX, AY, BX, BY, CX, CY}. En este ejemplo la regla dice: multiplicando 3 por 2 se obtiene 6.

Los conjuntos {A, B, C} y {X, Y} en este ejemplo son disjuntos, pero eso no es necesario. El número de formas de elegir un miembro de {A, B, C}, y después elegir otro, o sea, elegir un par ordenado de elementos elegidos de {A, B, C}, es 3 × 3 = 9.

En la teoría de conjuntos, este principio de multiplicación se toma a veces como la definición del producto de cardinales. Así,

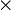|S_{1}|\cdot|S_{2}|\cdots|S_{n}| = |S_{1} \times S_{2} \times \cdots \times S_{n}|

donde \times es el producto cartesiano. Estos conjuntos no tienen por qué ser finitos, ni tampoco es necesario que haya un número finito de factores en el producto (véase número cardinal

Obtenido de "Regla del producto (Combinatoria)"

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Regla del producto — En combinatoria, la regla del producto es una regla de recuento básica. Enunciada de manera simple, es la idea de que si algo puede hacerse de a formas y otra cosa puede hacerse de b formas, entonces hay a · b formas de hacer ambas cosas. Así,… …   Enciclopedia Universal

  • Regla de la suma — Saltar a navegación, búsqueda En Combinatoria, la regla de la suma, es una de las Reglas de Conteo que existen. La Regla de la suma expresa que si dos eventos A y B, se llevan a cabo de manera secuencial, uno después de otro, donde A toma m pasos …   Wikipedia Español

  • Gottfried Leibniz — «Leibnitz» redirige aquí. Para el cráter lunar, véase Leibnitz (cráter lunar). Gottfried Leibniz. Gottfried Wilhelm Leibniz, a veces von Leibniz[1] (Leipzig …   Wikipedia Español

  • Emmy Noether — Amalie Emmy Noether Nacimiento 23 de marzo de 1882 Erlangen, Baviera, Alemania Fallecimiento …   Wikipedia Español

  • Permutación — Saltar a navegación, búsqueda En matemáticas, dado un conjunto finito con todos sus elementos diferentes, llamamos permutación a cada una de las posibles ordenaciones de los elementos de dicho conjunto. Por ejemplo, en el conjunto {1,2,3}, cada… …   Wikipedia Español

  • Matemática — Portal:Matemática Saltar a navegación, búsqueda     …   Wikipedia Español

  • Triángulo de Pascal — Este artículo o sección sobre matemáticas necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 16 de agosto de 2011. También puedes… …   Wikipedia Español

  • Coeficiente binomial — Los coeficientes binomiales o números combinatorios son una serie de números estudiados en combinatoria que indican el número de formas en que se pueden extraer subconjuntos a partir de un conjunto dado. Sin embargo, dependiendo del enfoque que… …   Wikipedia Español

  • Embriogénesis en Drosophila — Saltar a navegación, búsqueda …   Wikipedia Español

  • Poder disciplinario — Saltar a navegación, búsqueda El poder disciplinario es un concepto teórico desarrollado por Michel Foucault para describir el poder político desde un punto de vista antagónico al de la teoría clásica del poder. Contenido 1 Teoría clásica 2 El… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”