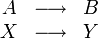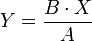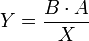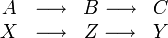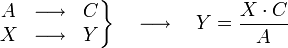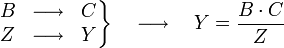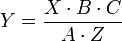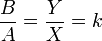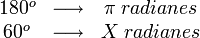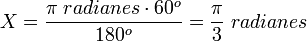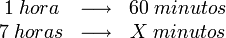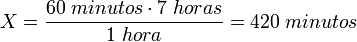Regla de tres

Regla de tres

Regla de tres

Regla de tres.svg

La regla de tres es una forma de resolución de problemas de proporcionalidad entre tres o más valores conocidos y una incógnita. En ella se establece una relación de linealidad (proporcionalidad) entre los valores involucrados.

La regla de tres más conocida es la regla de tres simple directa, si bien resulta muy práctico conocer la regla de tres simple inversa y la regla de tres compuesta, pues son de sencillo manejo y pueden utilizarse para la resolución de problemas cotidianos de manera efectiva.

Contenido

Regla de tres simple directa

Imaginemos que se nos plantea lo siguiente:

Problema a resolver: si necesito 3,5 litros de pintura para pintar 2 habitaciones, ¿cuántos litros necesito para pintar 7 habitaciones?

Este problema suele interpretarse de la siguiente manera:

2 habitaciones son a 3,5 litros como 7 habitaciones son a Y litros.

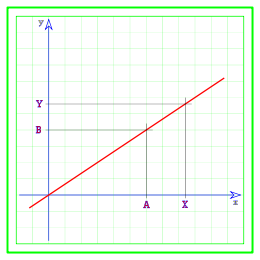
La solución es una "regla de tres simple directa": basta con multiplicar 7 por 3,5 y el resultado dividirlo entre 2. Necesitaré, por tanto, 12,25 litros de pintura. De manera formal, la regla de tres simple directa enuncia el problema de la siguiente manera:

A es a B como X es a Y

lo que suele representarse así:

\begin{matrix} A & \longrightarrow & B \\ X & \longrightarrow & Y \end{matrix}

donde A es 2, B es 3,5, X es 7 e Y es el término desconocido. Para resolver todas las reglas de tres simples directas basta con recordar la siguiente fórmula:

Y = \frac{B \cdot X}{A}

Regla de tres simple inversa

En la regla de tres simple inversa, cuando el tercer término (X) crece, también crece el término que intentamos averiguar (Y), y viceversa. En el ejemplo anterior, cuando el número de habitaciones aumenta, es obvio que necesitaremos más pintura, y cuando el número de habitaciones es menor, necesitaremos menos pintura. Es lo que se llama una relación directamente proporcional. Sin embargo la vida cotidiana puede ofrecer situaciones en las cuales la relación sea inversamente proporcional, es decir, si aumenta X, entonces Y disminuye, y viceversa. Veamos el siguiente ejemplo:

Problema a resolver: si 8 trabajadores construyen un muro en 10 horas, ¿cuánto tardarán 5 obreros en levantar el mismo muro?

Si se observa con atención el sentido del enunciado, resulta evidente que cuantos menos obreros trabajen, más horas necesitarán para levantar el mismo muro (suponiendo que todos trabajan a la misma velocidad). Tenemos por tanto una relación de proporcionalidad inversa, y deberemos aplicar una regla de tres simple inversa. Su resolución en este caso se plantea inicialmente de la misma forma, pero se resuelve de manera distinta. Al igual que antes, tenemos:

8 trabajadores son a 10 horas, como 5 trabajadores son a Y horas.

La solución pasa por multiplicar 8 por 10, y el resultado dividirlo por 5. Necesitarán, por tanto, 16 horas (nótese que si fuera una regla de tres directa hubiéramos operado multiplicando 5 por 10 y dividiendo el resultado por 8, lo que nos daría un resultado equivocado).

Formalizado, como antes:

A es a B como X es a Y

lo que se representa como:

\begin{matrix} A & \longrightarrow & B \\ X & \longrightarrow & Y \end{matrix}

Siendo la solución formalizada la siguiente (nótese el cambio de orden de los valores):

Y = \frac{B \cdot A}{X}

Es importante examinar con atención el enunciado para descubrir si se trata de una proporción directa o inversa.

Regla de tres compuesta

En ocasiones el problema planteado involucra más de tres cantidades conocidas, además de la desconocida. Observemos el siguiente ejemplo:

Problema a resolver: Si 12 trabajadores construyen un muro de 100 metros en 15 horas, ¿cuántos trabajadores se necesitarán para levantar un muro de 75 metros en 26 horas?

En el problema planteado aparecen dos relaciones de proporcionalidad al mismo tiempo. Además, para completar el ejemplo, se ha incluido una relación inversa y otra directa. En efecto, si un muro de 100 metros lo construyen 12 trabajadores, es evidente que para construir un muro de 75 metros se necesitarán menos trabajadores. Cuanto más pequeño es el muro, menos número de obreros precisamos: se trata de una relación de proporcionalidad directa. Por otro lado, si disponemos de 15 horas para que trabajen 12 obreros, es evidente que disponiendo de 26 horas necesitaremos menos obreros. Al aumentar una cantidad, disminuye la otra: se trata de una relación de proporcionalidad inversa.

El problema se enunciaría así:

100 metros son a 15 horas y 12 trabajadores como 75 metros son a 26 horas e Y trabajadores.

La solución al problema es multiplicar 12 por 75 y por 15, y el resultado dividirlo entre el producto de 100 por 26. Por tanto, 13500 entre 2600 resulta 5,19 (lo que por redondeo resultan ser 5 trabajadores).

Formalmente el problema se plantea así:

\begin{matrix} A & \longrightarrow & B \longrightarrow & C \\ X & \longrightarrow & Z \longrightarrow & Y \end{matrix}
  • La resolución implica plantear cada regla de tres simple por separado. Por un lado, la primera, que, recordemos, es directa, y se resuelve así:
\left . \begin{matrix} A & \longrightarrow & C \\ X & \longrightarrow & Y \end{matrix} \right \} \quad \longrightarrow \quad Y = \frac{X \cdot C}{A}
  • A continuación planteamos la segunda, que, recordemos, es inversa, y se resuelve así:
\left . \begin{matrix} B & \longrightarrow & C \\ Z & \longrightarrow & Y \end{matrix} \right \} \quad \longrightarrow \quad Y = \frac{B \cdot C}{Z}
  • A continuación unimos ambas operaciones en una sola, teniendo cuidado de no repetir ningún término (es decir, añadiendo el término C una sola vez):
Y = \frac{X \cdot B \cdot C}{A \cdot Z}

lo que nos da la solución buscada.

El problema se puede plantear con todos los términos que se quiera, sean todas las relaciones directas, todas inversas o mezcladas, como en el caso anterior. Cada regla ha de plantearse con sumo cuidado, teniendo en cuenta si es inversa o directa, y teniendo en cuenta (esto es muy importante) no repetir ningún término al unir cada una de las relaciones simples.

Campo de aplicación

Como se ha comentado, la regla de tres es un mecanismo sencillo y extremadamente útil que sólo se puede establecer cuando existe una relación de linealidad entre los valores que pueden tomar las variables que intervienen. Sin embargo no es siempre fácil averiguar si existe tal relación, de modo que es necesario utilizar para ello el sentido común y la experiencia.

Demostración

La regla de tres se fundamenta en una relación de proporcionalidad. Una cantidad es a otra, como una tercera lo es a una cuarta. Como ya se ha comentado, la regla de tres establece una relación de proporcionalidad, por lo que rápidamente se observa que:

\frac{B}{A} = \frac{Y}{X} = k

Donde k es la constante de proporcionalidad, despejando se obtiene que:

Y = \frac{B \cdot X}{A}

Ejemplos

  • Para pasar 60 grados a radianes podríamos establecer la siguiente regla de tres:

Ubicamos la incógnita en la primera posición:

\begin{matrix} 180^o & \longrightarrow & \pi \; radianes \\ 60^o & \longrightarrow & X \; radianes \end{matrix}

Esto formaliza la pregunta "¿Cuántos radianes hay en 60 grados, dado que π radianes son 180 grados?". Así tenemos que:

X = \frac{\pi \; radianes \cdot 60^o}{180^o}= \frac{\pi}{3} \; radianes

Donde π es el Número π.

Una técnica útil para recordar cómo encontrar la solución de una regla de tres es la siguiente: X es igual al producto de los términos cruzados (π y 60, en este caso) dividido por el término que está frente a X.

  • Calcular cuántos minutos hay en 7 horas. Sabemos que hay 60 minutos en 1 hora, por lo que escribimos:
\begin{matrix} 1 \; hora & \longrightarrow & 60 \; minutos \\ 7 \; horas & \longrightarrow & X \; minutos \end{matrix}

El resultado es:

X = \frac {60 \; minutos \cdot 7 \; horas} {1 \; hora} = 420 \; minutos

Enlaces externos

Obtenido de "Regla de tres"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Regla de tres — ► locución MATEMÁTICAS Cálculo de una magnitud desconocida a partir de otras tres conocidas, dos de las cuales varían en proporción directa o inversa. * * * La regla de tres es una relación que se establece entre tres (o más) valores conocidos y… …   Enciclopedia Universal

  • regla — (Del lat. regŭla). 1. f. Instrumento de madera, metal u otra materia rígida, por lo común de poco grueso y de forma rectangular, que sirve principalmente para trazar líneas rectas, o para medir la distancia entre dos puntos. 2. Aquello que ha de… …   Diccionario de la lengua española

  • regla — sustantivo femenino 1. Área: dibujo Instrumento rectangular alargado y con base plana que sirve para trazar líneas rectas o para medir distancias en el papel: Déjame la regla para dibujar una torre. Puedes saber los kilómetros que hay entre dos… …   Diccionario Salamanca de la Lengua Española

  • tres — (Del lat. tres). 1. adj. Dos y uno. 2. tercero (ǁ ordinal). Número tres. Año tres. Apl. a los días del mes, u. t. c. s. [m6]El tres de julio. 3. m. Signo o conjunto de signos con que se representa el número tres. 4. Carta o naipe que tiene …   Diccionario de la lengua española

  • Regla — (Del lat. regula.) ► sustantivo femenino 1 Instrumento hecho de material rígido de forma rectangular que sirve para trazar líneas rectas o para medir la distancia entre dos puntos: ■ para hacer dibujo lineal es imprescindible una regla. SINÓNIMO… …   Enciclopedia Universal

  • regla — {{＃}}{{LM R33461}}{{〓}} {{SynR34288}} {{［}}regla{{］}} ‹re·gla› {{《}}▍ s.f.{{》}} {{＜}}1{{＞}} Instrumento de forma rectangular y alargada que se utiliza principalmente para trazar líneas rectas o para medir la distancia entre dos puntos: • Las… …   Diccionario de uso del español actual con sinónimos y antónimos

  • Tres — (Del lat. tres.) ► adjetivo numeral/ sustantivo masculino 1 Que resulta de la suma de dos y uno: ■ tres más uno son cuatro. ► adjetivo numeral/ sustantivo masculino femenino 2 Que ocupa la tercera posición en una serie. ► sustantivo masculino 3… …   Enciclopedia Universal

  • règla — règlo f. règle; statut; loi; précepte > Es de règla que… : il est de règle que. Una règla de tres : une règle de trois. Èstre en règla, si metre en règla : être en règle ; se mettre en règle. Lei règlas d una frema : les menstrues. voir… …   Diccionari Personau e Evolutiu

  • Tres — Para otros usos de este término, véase Tres (desambiguación). 3 Cardinal Tres Ordinal Tercero, a Factorización 3 (núme …   Wikipedia Español

  • Regla de cálculo — Saltar a navegación, búsqueda La regla de cálculo es un instrumento manual de cálculo que dispone de varias escalas numéricas, para facilitar la rápida y cómoda realización de operaciones aritméticas complejas, como puedan ser multiplicaciones,… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”