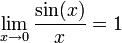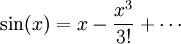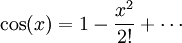- Radián
-
Radián
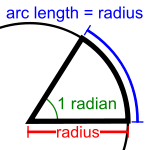
El radián es la unidad de ángulo plano en el Sistema Internacional de Unidades. Representa el ángulo central en una circunferencia que subtiende un arco cuya longitud es igual a la del radio. Su símbolo es rad.
Hasta 1995 tuvo la categoría de unidad suplementaria en el Sistema Internacional de Unidades, junto con el estereorradián. A partir de ese año, y hasta el momento presente, ambas unidades figuran en a la categoría de unidades derivadas.
Esta unidad se utiliza primordialmente en la Física, el cálculo infinitesimal, la trigonometría, la goniometría, etc.
Contenido
Historia
El término radián surge en unas preguntas de examen propuestas por James Thomson, hermano de Lord Kelvin, en el Queen's College de Belfast. James Thomson usó el término ya en 1871, como variante de rad, radial y radián.
Definición
El radián se define como el ángulo central que limita un arco de circunferencia cuya longitud es igual a la del radio de la circunferencia.
Así, el ángulo formado por dos radios de una circunferencia, medido en radianes, es igual a la longitud del arco que delimitan los radios; es decir, θ = s /r, donde θ es ángulo, s es la longitud del arco, y r es el radio. Por tanto, el ángulo completo α, de una circunferencia de radio r, medido en radianes, es:
Utilidad
Ángulos de los polígonos más comunes medidos en radianes, expresados como fracciones de π.
El radián es una unidad sumamente útil para medir ángulos, puesto que simplifica los cálculos, ya que los más comunes se expresan mediante sencillos múltiplos o divisores de π.
Análisis dimensional
El radián es la unidad natural en la medida de los ángulos. Por ejemplo, la función seno de un ángulo x expresado en radianes cumple:
Análogamente los desarrollos Taylor de las funciones seno y coseno son:
donde x se expresa en radianes.
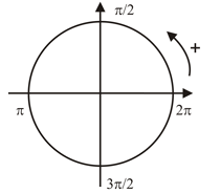
Equivalencias
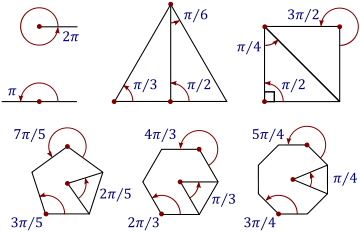
Tabla de conversión entre grados sexagesimales y radianesLa equivalencia entre grados sexagesimales y radianes es: π rad = 180°
La tabla muestra la conversión de los ángulos más comunes.
Grados 0° 30° 45° 60° 90° 180° 270° 360° Radianes 0 π/6 π/4 π/3 π/2 π 3π/2 2π Otras unidades de medida de ángulos convencionales son el grado sexagesimal, el grado centesimal y, en astronomía, la hora.
Véase también
Referencias
Bibliografía
- Florian Cajori, 1929, History of Mathematical Notations, Vol. 2, pp. 147–148; Nature, 1910, Vol. 83, pp. 156, 217, and 459–460;
Categorías: Unidades derivadas del Sistema Internacional | Unidades de ángulo
Wikimedia foundation. 2010.
