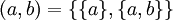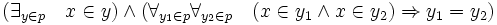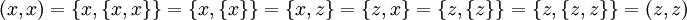Par ordenado

Par ordenado

Par ordenado

Un par ordenado es una tupla de dos elementos, tal que uno puede ser distinguido como el primero y el otro como el segundo. Un par ordenado con primer elemento a y segundo b es escrito usualmente como (a, b). Dos pares ordenados cumplen:

(a, b) = (c, d) si y sólo si a = c y b = d

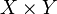El conjunto de todos los pares ordenados en los cuales el primer elemento se toma de un conjunto X determinado y el segundo de un conjunto Y se llama producto cartesiano de X e Y, escrito X \times Y.

Tuplas ordenadas

Los tríos ordenados y las tuplas ordenadas se pueden definir recursivamente a partir de la definición de par ordenado: un trío ordenado (a,b,c) puede ser definido como (a,(b,c)) ó como ((a,b),c); o sea, un par ordenado que contiene otro par ordenado como elemento.

Esta aproximación se refleja en lenguajes de programación: es posible representar una lista de elementos como una construcción de pares ordenados anidados. Por ejemplo, la lista (1,2,3,4,5) se convierte en (1,(2,(3,(4,(5,()))))). El lenguaje de programación Lisp usa estas listas como su estructura de datos primaria.

Pares ordenados en la teoría de conjuntos

En la teoría de conjuntos pura, donde solamente existen conjuntos, pares ordenados (a, b) se pueden definir como el conjunto:

~(a,b)=\{\{a\},\{a,b\}\}

Esta definición tiene el nombre de par de Kuratowski, y es bien básica, porque requiere de apenas pocos axiomas para poder ser formulada (el axioma de extensión, el axioma de separación y el axioma del par).

La afirmación de que x sea el primer elemento de un par ordenado p puede ser entonces formulada como

\forall_{y\in p}\qquad x\in y

y que x sea el segundo elemento de p como

(\exist_{y\in p}\quad x\in y)\wedge(\forall_{y_1\in p}\forall_{y_2\in p}\quad (x \in y_1 \wedge x\in y_2) \Rightarrow y_1=y_2)

Nótese que esta definición también es válida para el par ordenado p = (x,x) = {{x},{x,x}} = {{x},{x}} = {{x}}.

En la formulación usual ZF de la teoría de conjuntos incluyendo el axioma de regularidad, un par ordenado (a,b) puede también ser definido como el conjunto {a,{a,b}}. De todas formas, el axioma de regularidad es necesario, dado que sin él, sería posible considerar conjuntos x y z tales que x = {z},z = {x}, y 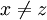x\neq z. Entonces se tendría que

(x,x)=\{x,\{x,x\}\}=\{x,\{x\}\}=\{x,z\}=\{z,x\}=\{z,\{z\}\}=\{z,\{z,z\}\}=(z,z)\,

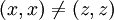mientras que se quiere que (x,x)\neq(z,z).

Obtenido de "Par ordenado"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Par ordenado — Un par ordenado es una tupla ordenada de dos elementos, separados por una coma: (a, b). Como es ordenado, no es lo mismo (a, b) que (b, a). Las partes de un par ordenado son: ● Primer conjunto, primer componente; ● Segundo conjunto, segundo… …   Enciclopedia Universal

  • ordenado — ordenado, da adjetivo 1. Que hace las cosas con orden: Tu hermana es una persona muy ordenada. Locuciones 1. par* ordenado …   Diccionario Salamanca de la Lengua Española

  • Par — o PAR puede referirse a: Contenido 1 Acrónimo 2 Biografías 3 Biología 4 Cultura 5 Física …   Wikipedia Español

  • par — adjetivo,sustantivo masculino 1. [Número] que es exactamente divisible por dos: Los números pares son divisibles por dos, los impares no. número par. adjetivo 1. [Órgano] …   Diccionario Salamanca de la Lengua Española

  • Par fundamental de períodos — Saltar a navegación, búsqueda En el ámbito de las matemáticas, un par fundamental de períodos es un par ordenado de números complejos que define una grilla en el plano complejo. Este tipo de grilla es el objeto a partir del cual se definen las… …   Wikipedia Español

  • Álgebra de las palabras — El álgebra de las palabras estudia la formalización gramatical de las construcciones de palabras sobre un alfabeto para un lenguaje, desde una perspectiva matemática que nos permita, de un modo firme, afirmar o rechazar diversos resultados… …   Wikipedia Español

  • Número real — Diferentes clases de números reales. Recta real …   Wikipedia Español

  • Operación externa — Se dice que esta Operación matemática es una operación externa o una Ley de composición externa si la aplicación entre los conjuntos es de la forma: siendo la operación binaria, que representamos …   Wikipedia Español

  • Relación de orden — Saltar a navegación, búsqueda Sea A un conjunto dado no vacío y R una relación binaria definida en A, entonces decimos que R es una relación de orden si cumple las siguientes propiedades: Reflexividad: Todo elemento de A está relacionado consigo… …   Wikipedia Español

  • Tupla — Una tupla, en matemáticas, es una secuencia ordenada de objetos, esto es, una lista con un número limitado de objetos (una secuencia infinita se denomina en matemática como una familia). Las tuplas se emplean para describir objetos matemáticos… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”