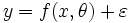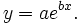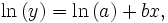En estadística, la regresión no lineal es un problema de inferencia para un modelo tipo:

basado en datos multidimensionales x,y, donde f es alguna función no lineal respecto a algunos parámetros desconocidos θ. Como mínimo, se pretende obtener los valores de los parámetros asociados con la mejor curva de ajuste (habitualmente, con el método de los mínimos cuadrados). Con el fin de determinar si el modelo es adecuado, puede ser necesario utilizar conceptos de inferencia estadística tales como intervalos de confianza para los parámetros así como pruebas de bondad de ajuste.

El objetivo de la regresión no lineal se puede clarificar al considerar el caso de la regresión polinomial, la cual es mejor no tratar como un caso de regresión no lineal. Cuando la función f toma la forma:

f(x) = ax² + bx + c

la función f es no lineal en función de x pero lineal en función de los parámetros desconocidos a, b, yc. Este es el sentido del término "lineal" en el contexto de la regresión estadística. Los procedimientos computacionales para la regresión polinomial son procedimientos de regresión lineal (múltiple), en este caso con dos variables predictoras x y x². Sin embargo, en ocasiones se sugiere que la regresión no lineal es necesaria para ajustar polinomios. Las consecuencias practicas de esta mala interpretación conducen a que un procedimiento de optimización no lineal sea usado cuando en realidad hay una solución disponible en términos de regresión lineal. Paquetes (software) estadísticos consideran, por lo general, más alternativas de regresión lineal que de regresión no lineal en sus procedimientos.

Contenido 1 General 1.1 Linealización 1.2 Mínimos cuadrados ordinarios y ponderados 1.3 Estimación de los parámetros usando Métodos de Monte Carlo 1.4 Software 2 Referencias 3 Notas 4 Véase también 5 Enlaces externos

General

Linealización

Algunos problemas de regresión no lineal pueden linealizarse mediante una transformación en la formulación del modelo. Por ejemplo, consideremos el problema de regresión no lineal (ignorando el término de error):

Aplicando logaritmos a ambos lados de la ecuación, se obtiene:

lo cual sugiere una estimación de los parámetros desconocidos a través de un modelo de regresión lineal de ln(y) con respecto a x, un calculo que no requiere procedimientos de optimización iterativa. De todas formas, la linealización debe usarse con cuidado ya que la influencia de los datos en el modelo cambia, así como la estructura del error del modelo y la interpretación e inferencia de los resultados. Estos pueden ser resultados no muy convenientes.

Hay que distinguir entre la "linealización" usada en los párrafos anteriores y la "linealización local" que se adopta para algoritmos clásicos como el de Gauss-Newton. De igual forma, la metodología de modelos lineales generalizados no use linealización para la estimación de parámetros.

Mínimos cuadrados ordinarios y ponderados

La mejor curva de ajuste se considera como aquella que minimiza la suma de las desviaciones (residuales) al cuadrado (SRC). Este es la aproximación por el método de mínimos cuadrados (MMC). Sin embargo, en aquellos casos donde se tienen diferentes varianzas de error para diferentes errores, es necesario minimizar la suma de los residuales al cuadrado ponderados (SRCP) (método de mínimos cuadrados ponderados). En la practica, la varianza puede depender del valor promedio ajustado. Así que los pesos son recalculados para cada iteración en un algoritmo de mínimos cuadrados ponderados iterativo.

En general, no hay una expresión de forma cerrada para los parámetros de mejor ajuste, como sucede en el caso de la regresión lineal. Métodos numéricos de optimización son aplicados con el fin de determinar los parámetros de mejor ajuste. Otra vez, en contraste con la regresión lineal, podría haber varios máximos locales de la función a ser optimizada. En la práctica, se suponen algunos valores iniciales los cuales junto con el algoritmo de optimización conducen a encontrar el máximo global.

Estimación de los parámetros usando Métodos de Monte Carlo

Si el error de cada observación es conocido, entonces la precisión y confiabilidad de los parámetros puede ser estimada mediante simulación de Monte Carlo. Cada observación es aleatorizada de acuerdo a su media y su desviación estándar. Con el nuevo conjunto de datos, una nueva curva es ajustada y las estimaciones de los parámetros registradas. Las observaciones son entonces aleatorizadas y nuevos valores de los parámetros son obtenidos. Al final, varios conjuntos de parámetros son generados y su media y desviación estándar pueden ser calculados.^{[1] [2]}

Software

Diversos lenguajes de programación y software estadístico y matemático contienen funciones de optimización. Entre ellos, Gauss, GNU Octave, Matlab, Mathematica, R, Splus; C++ y Fortran maple.

Referencias

• G.A.F Seber and C.J. Wild. Nonlinear Regression. New York: John Wiley and Sons, 1989.
• R.M. Bethea, B.S. Duran and T.L. Boullion. Statistical Methods for Engineers and Scientists. New York: Marcel Dekker, Inc 1985 ISBN 0-8247-7227-X

Notas

1. ↑ Motulsky, HJ & Ransnas, LA (1987) Fitting curves to data using nonlinear regression. FASEB J 1:365-374
2. ↑ McIntosh, JEA & McIntosh, RP (1980) Mathematical modelling and computers in endocrinology. p71 Springer-Verlag, Berlin, Germany.

Véase también

• Algoritmo de Levenberg-Marquardt
• Algoritmo de Gauss-Newton
• Análisis de la regresión
• Regresión lineal
• Regresión logística

Enlaces externos

• Arquimedex.com, Ajuste de funciones por regresión OnLine (en español)
• ISAT, Nonlinear regression with explicit error control
• Zunzun.com, Online curve and surface fitting
• NLREG, a proprietary program
• Matlab statistic