- Método de Monte Carlo
-
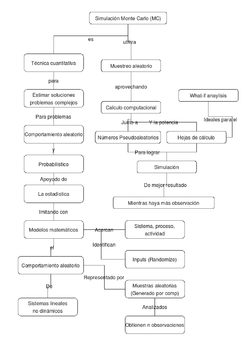
Método de Monte Carlo
El método de Monte Carlo es un método no determinístico o estadístico numérico usado para aproximar expresiones matemáticas complejas y costosas de evaluar con exactitud. El método se llamó así en referencia al Casino de Montecarlo (Principado de Mónaco) por ser “la capital del juego de azar”, al ser la ruleta un generador simple de números aleatorios. El nombre y el desarrollo sistemático de los métodos de Monte Carlo datan aproximadamente de 1944 y se mejoraron enormemente con el desarrollo de la computadora.
El uso de los métodos de Monte Carlo como herramienta de investigación, proviene del trabajo realizado en el desarrollo de la bomba atómica durante la segunda guerra mundial en el Laboratorio Nacional de Los Álamos en EE.UU. Este trabajo conllevaba la simulación de problemas probabilísticos de hidrodinámica concernientes a la difusión de neutrones en el material de fusión, la cual posee un comportamiento eminentemente aleatorio. En la actualidad es parte fundamental de los algoritmos de trazado de rayos para la generación de imágenes sintéticas.
En la primera etapa de estas investigaciones, John von Neumann y Stanislaw Ulam refinaron esta ruleta rusa y los métodos "de división" de tareas. Sin embargo, el desarrollo sistemático de estas ideas tuvo que esperar al trabajo de Harris y Herman Kahn en 1948. Aproximadamente en el mismo año, Enrico Fermi, Metropolis y Ulam obtuvieron estimadores para los valores característicos de la ecuación de Schrödinger para la captura de neutrones a nivel nuclear usando este método.
El método de Monte Carlo proporciona soluciones aproximadas a una gran variedad de problemas matemáticos posibilitando la realización de experimentos con muestreos de números pseudoaleatorios en una computadora. El método es aplicable a cualquier tipo de problema, ya sea estocástico o determinista. A diferencia de los métodos numéricos que se basan en evaluaciones en N puntos en un espacio M-dimensional para producir una solución aproximada, el método de Monte Carlo tiene un error absoluto de la estimación que decrece como
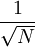 en virtud del teorema del límite central.
en virtud del teorema del límite central.Contenido
Orígenes del método
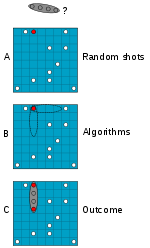
La invención del método de Monte Carlo se asigna a Stan Ulam y a John von Neumann. Ulam ha explicado cómo se le ocurrió la idea mientras jugaba un solitario durante una enfermedad en 1946. Advirtió que resulta mucho más simple tener una idea del resultado general del solitario haciendo pruebas múltiples con las cartas y contando las proporciones de los resultados que computar todas las posibilidades de combinación formalmente. Se le ocurrió que esta misma observación debía aplicarse a su trabajo de Los Álamos sobre difusión de neutrones, para la cual resulta prácticamente imposible solucionar las ecuaciones íntegro-diferenciales que gobiernan la dispersión, la absorción y la fisión. “La idea consistía en probar con experimentos mentales las miles de posibilidades, y en cada etapa, determinar por casualidad, por un número aleatorio distribuido según las probabilidades, qué sucedería y totalizar todas las posibilidades y tener una idea de la conducta del proceso físico”.
Podían utilizarse máquinas de computación, que comenzaban a estar disponibles, para efectuar las pruebas numéricas y en efecto reemplazar el aparato experimental del físico. Durante una de las visitas de von Neumann a Los Álamos en 1946, Ulam le mencionó el método. Después de cierto escepticismo inicial, von Neumann se entusiasmó con la idea y pronto comenzó a desarrollar sus posibilidades en un procedimiento sistemático. Ulam expresó que Monte Carlo “comenzó a tener forma concreta y empezó a desarrollarse con todas sus fallas de teoría rudimentaria después de que se lo propuse a Johnny”.
A principios de 1947 Von Neumann envió una carta a Richtmyer a Los Álamos en la que expuso de modo influyente tal vez el primer informe por escrito del método de Monte Carlo. Su carta fue encuadernada junto con la respuesta de Richtmyer como un informe de Los Álamos y distribuida entre los miembros del laboratorio. Von Neumann sugería aplicar el método para rastrear la generación isótropa de neutrones desde una composición variable de material activo a lo largo del radio de una esfera. Sostenía que el problema era adecuado para el ENIAC y estimaba que llevaría 5 horas calcular la acción de 100 neutrones a través de un curso de 100 colisiones cada uno.
Ulam estaba particularmente interesado en el método Monte Carlo para evaluar integrales múltiples. Una de las primeras aplicaciones de este método a un problema determinista fue llevada a cabo en 1948 por Enrico Fermi, Ulam y von Neumann cuando consideraron los valores singulares de la ecuación de Schrödinger.
Ejemplo
Si deseamos reproducir, mediante números aleatorios, la tirada sucesiva de una moneda, debemos previamente asignarle un intervalo de números aleatorios a CARA y otro a CRUZ, de manera de poder interpretar el resultado de la simulación. Tales intervalos se asignan en función de las probabilidades de ocurrencia de cada cara de la moneda. Tenemos así:
CARA Probabilidad: 0,50 Números aleatorios: 0,000 al 0,499CRUZ Probabilidad: 0,50 Números aleatorios: 0,500 al 0,999
Después, al generar un número aleatorio a partir de la función RAN de la calculadora, por ejemplo, obtenemos el resultado simulado. Así, si obtenemos el número aleatorio 0,385, observamos que está incluido en el intervalo asignado a CARA.En otras aplicaciones, se asocian intervalos de números aleatorios según las probabilidades de ocurrencia de los eventos a simular.
Bibliografía
“John von Neumann y los orígenes de la computación moderna” de William Aspray – Gedisa Editorial - 1992
Véase también
 Portal:Matemática Contenido relacionado con Matemática.
Portal:Matemática Contenido relacionado con Matemática.- Cadena de Márkov
- Integración de Monte Carlo
- Método quasi-Monte Carlo
- Azar
- Algoritmo de Las Vegas
- Generador de números aleatorios
- Estocástico
Enlaces externos
- Economía Excel Aplicaciones del método de Monte Carlo con Excel.
- SimulAr Software gratuito de Simulación de Monte Carlo con Excel.
Categoría: Método de Monte Carlo
Wikimedia foundation. 2010.