ÁRBOLES AVL.

El problema que tiene el Árbol binario de búsqueda es que pueden producirse árboles degenerados o parcialmente degenerados, por lo que la búsqueda de un elemento puede llegar a ser de un orden de 0(lg n) y en el peor caso llegar a tener un orden de 0(n).

Gracias a los científicos Giorgii Adelson – Velsky y Yevgeniy Mikhailovich Landis, quedó resuelto este problema ya que idearon los árboles AVL, nombrados de esta forma en su honor, o balanceados en altura.

El árbol AVL es, en computación, Árbol binario de búsqueda el cual es un árbol o bien vacío o bien un árbol binario con hijo izquierdo e hijo derecho que son a su vez AVL, y además la diferencia entre sus alturas es menor o igual que 1.En este tipo de árboles, la búsqueda del elemento puede tener una complejidad de 0(log (n)).

Teorema de AVL

Gn = nº nodos en el AVL de altura n que tiene menos nodos

Entonces: Gn = Gn-1 + Gn-2 +1

OPERACIONES.

Los árboles AVL comparten las mismas operaciones básicas que el Árbol binario de búsqueda. Para conseguir un factor de balance óptimo (diferencia entre las alturas de sus subárboles izquierdo y derecho), es decir, que se encuentre entre los límites establecidos lo conseguiremos con los procesos de inserción y eliminación, junto con las rotaciones hacia la izquierda y hacia la derecha.

BALANCE DEL ÁRBOL.

El inconveniente que presentan estos árboles, es que al realizar modificaciones sobre él (insertar o borrar) podemos perder el equilibrio, por lo que tendremos que proceder al equilibrado del árbol mediante rotaciones.

ROTACIONES.

El reequilibrado se produce de abajo hacia arriba sobre los nodos en los que se produce el desequilibrio. Pueden darse dos casos: rotación simple o rotación doble; a su vez ambos casos pueden ser hacia la derecha o hacia la izquierda.

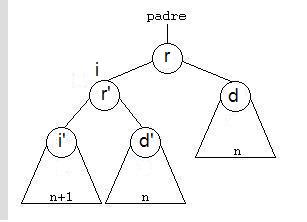
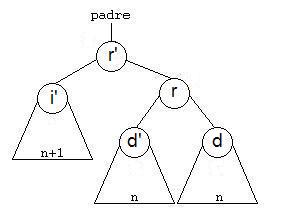
ROTACIÓN SIMPLE A LA DERECHA.

De un árbol de raíz (r) y de hijos izquierdo (i) y derecho (d), lo que haremos será formar un nuevo árbol cuya raíz sea la raíz del hijo izquierdo, como hijo izquierdo colocamos el hijo izquierdo de i (nuestro i’) y como hijo derecho construimos un nuevo árbol que tendrá como raíz, la raíz del árbol (r), el hijo derecho de i (d’) será el hijo izquierdo y el hijo derecho será el hijo derecho del árbol (d).

op rotDer: AVL{X} -> [AVL{X}] .
eq rotDer(arbolBin(R1, arbolBin(R2, I2, D2), D1)) ==
arbolBin(R2, I2, arbolBin(R1, D2, D)) .

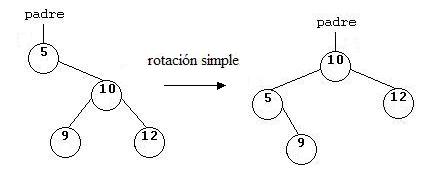
ROTACIÓN SIMPLE A LA IZQUIERDA.

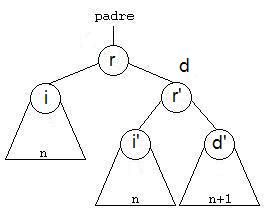
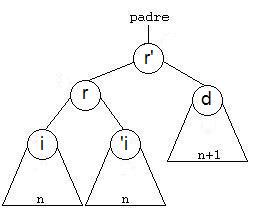
De un árbol de raíz (r) y de hijos izquierdo (i) y derecho (d), consiste en formar un nuevo árbol cuya raíz sea la raíz del hijo derecho, como hijo derecho colocamos el hijo derecho de d (nuestro d’) y como hijo izquierdo construimos un nuevo árbol que tendrá como raíz la raíz del árbol (r), el hijo izquierdo de d será el hijo derecho (i’) y el hijo izquierdo será el hijo izquierdo del árbol (i).

Precondición : Tiene que tener hijo derecho no vacío.

 op rotIzq: AVL{X} -> [AVL{X}] .
eq rotIzq(arbolBin(R1, I, arbolBin(R2, I2, D2))) ==
arbolBin(R2, arbolBin(R1, I, I2), D2) .

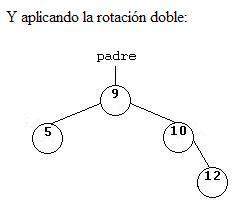
Si la inserción se produce en el hijo derecho del hijo izquierdo del nodo desequilibrado (o viceversa) hay que realizar una doble rotación.

ROTACIÓN DOBLE A LA DERECHA.

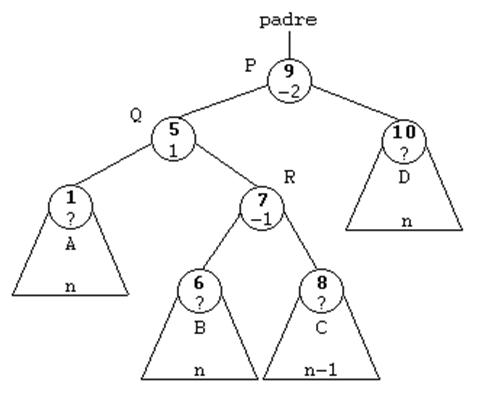
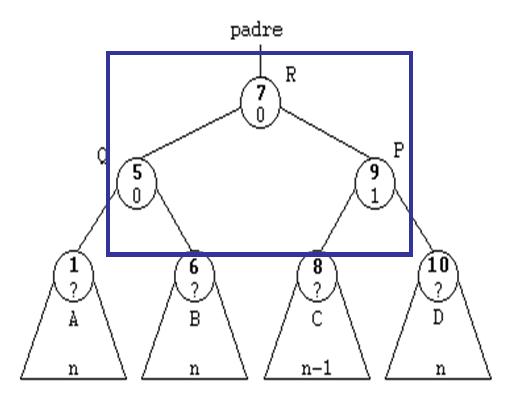
ROTACIÓN DOBLE A LA IZQUIERDA.

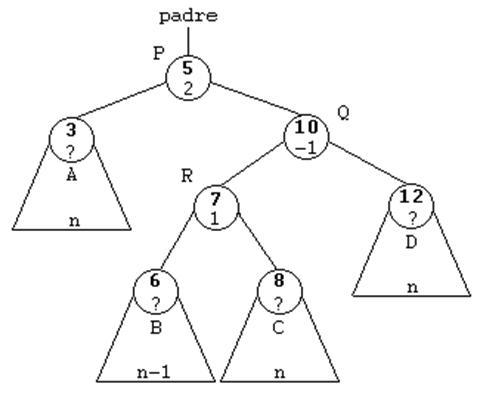
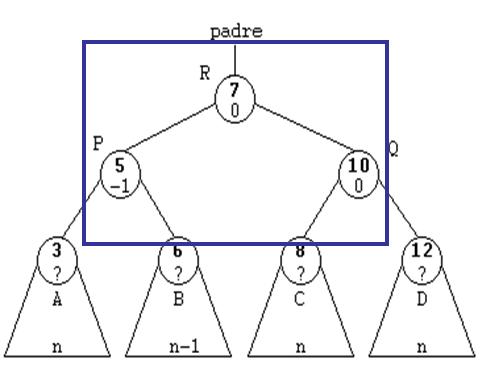
INSERCIÓN.

La inserción de un elemento en un árbol AVL es idéntica que en un árbol binario de búsqueda, la diferencia se encuentra en la comprobación que hay que realizar posteriormente en los árboles AVL. En un árbol AVL tras realizar la inserción hay que comprobar que se sigue manteniendo la condición de equilibrio, o lo que es lo mismo, que la altura del subárbol izquierdo y la del subárbol derecho difieran en una unidad o sean iguales. Si se produce un desequilibrio hay que reequilibrar la estructura para que siga siendo un árbol AVL.

Debido a que las rotaciones son una operación que tienen complejidad constante y a que la altura esta limitada a O (log(n)), el tiempo de ejecución para la inserción es del orden O (log(n)).

op insertar: X$Elt AVL{X} -> AVLNV{X} .
eq insertar(R, crear) == arbolBin(R, crear, crear) .
	ceq insertar(R1, arbolBin(R2, I, D)) ==
if (R1==R2) then
			arbolBin(R2, I, D)
		elseif (R1<R2) then
			if ( (altura(insertar(R1,I)) – altura(D)) < 2) then
				arbolBin(R2, insertar(R1, I), D)
			else ***hay que reequilibrar
				if (R1 < raiz(I)) then
					rotarDer(arbolBin(R2, insertar(R1, I), D))
				else
					rotarDer(arbolBin(R2, rotarIzq(insertar(R1, I)), D))
				fi .
			fi .
		else
			if ( (altura(insertar(R1,I)) – altura(D)) < 2) then
				arbolBin(R2, insertar(R1, I), D)
			else *** hay que reequilibrar
				if (R1 > raiz(D)) then
					rotarIzq(arbolBin(R, I, insertar(R1, D)))
				else
					rotatIzq(arbolBin(R, I, rotarDer(insertar(R1, D))))
				fi .
			fi .
		fi .

BORRADO.

En esta operación lo primero que haremos será buscar el elemento que deseamos eliminar, y una vez encontrado procederemos a su borrado, para lo cual se distinguen los siguientes casos:

Que el nodo a eliminar sea:

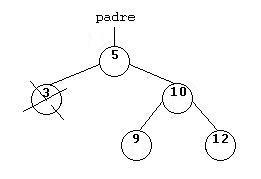
1. Una hoja, por lo que simplemente, lo eliminaremos sin realizar más operaciones.

2. Posea un solo hijo, con lo que el padre del elemento que queremos eliminar, apuntará al hijo del elemento que deseamos borrar.

3. Posea dos hijos, por lo que procederemos de la siguiente forma: Buscamos el elemento mínimo del hijo derecho, una vez encontrado, sustituimos el elemento a eliminar por dicho elemento y lo eliminamos del hijo derecho, en último lugar observaremos el equilibrio del árbol y procederemos según convenga.

op eliminar: X$Elt AVL{X} -> AVL{X} .
eq eliminar(R, crear) == crear .
ceq eliminar(R1, arbolBin(R2, I, D)) ==
	if (R1 == R2) then
		if esVacio(I) then
			D
		elseif esVacio(D) then
			I
		else
			if (altura(I) - altura(eliminar(min(D),D)) < 2) then
				arbolBin(min(D), I, eliminar(min(D), D))
			***tenemos que reequilibrar
			elseif (altura(hijoIzq(I) >= altura(hijoDer(I)))) then
				rotDer(arbolBin(min(D), I, eliminar(min(D),D)))
			else
   rotDer(arbolBin(min(D), rotIzq(I), eliminar(min(D),D)))

BÚSQUEDA.

La búsqueda en un árbol AVL se implementa igual que en el Árbol binario de búsqueda, pero con la mejora de que al ser diferentes respecto a la altura, tienen una complejidad del orden de 0(log (n)).

Especificación completa, en lenguaje MAUDE

fmod ARBOL-AVL {X :: ORDEN} is
 
protecting ARBOL-BINARIO-BUSQUEDA{X} .
sorts AVL{X} AVLNV{X} .
subsort AVLNV{X} < AVL{X} .
subsort AVL{X} < ABB{X} .
subsort AVLNV{X} < ABBNV{X} .
 
	***precondiciones
var ANV : ABBNV{X} .
vars R R1 R2 : X$Elt .
vars I D I1 I2 D1 D2: AVL{X} .
 
mb crear : AVL{X} .
cmb ANV : AVLNV{X} if sd(altura(hijoIzq(ANV)), altura(hijoDer(ANV))) <= 1 .
 
	***constructores
op hijoIzq: AVLNV{X} -> AVL{X} .
op hijoDer: AVLNV{X} -> AVL{X} .
eq hijoIzq(arbolBin(R, I, D)) == I .
eq hijoDer(arbolBin(R, I, D)) == D .
 
op insertar: X$Elt AVL{X} -> AVLNV{X} .
eq insertar(R, crear) == arbolBin(R, crear, crear) .
	ceq insertar(R1, arbolBin(R2, I, D)) ==
if (R1==R2) then
			arbolBin(R2, I, D)
		elseif (R1<R2) then
			if ( (altura(insertar(R1,I)) – altura(D)) < 2) then
				arbolBin(R2, insertar(R1, I), D)
			else ***hay que reequilibrar
				if (R1 < raiz(I)) then
					rotarDer(arbolBin(R2, insertar(R1, I), D))
				else
					rotarDer(arbolBin(R2, rotarIzq(insertar(R1, I)), D))
				fi .
			fi .
		else
			if ( (altura(insertar(R1,I)) – altura(D)) < 2) then
				arbolBin(R2, insertar(R1, I), D)
			else *** hay que reequilibrar
				if (R1 > raiz(D)) then
					rotarIzq(arbolBin(R, I, insertar(R1, D)))
				else
					rotatIzq(arbolBin(R, I, rotarDer(insertar(R1, D))))
				fi .
			fi .
		fi .
op eliminar: X$Elt AVL{X} -> AVL{X} .
eq eliminar(R, crear) == crear .
ceq eliminar(R1, arbolBin(R2, I, D)) ==
	if (R1 == R2) then
		if esVacio(I) then
			D
		elseif esVacio(D) then
			I
		else
			if (altura(I) - altura(eliminar(min(D),D)) < 2) then
				arbolBin(min(D), I, eliminar(min(D), D))
			***tenemos que reequilibrar
			elseif (altura(hijoIzq(I) >= altura(hijoDer(I)))) then
				rotDer(arbolBin(min(D), I, eliminar(min(D),D)))
			else
   rotDer(arbolBin(min(D), rotIzq(I), eliminar(min(D),D)))
fi .
			fi .
		elseif (R1 < R2) then
			if(altura(D) – altura(eliminar(R1,I)) <= 1) then
				arbolBin(R2, eliminar(R1,I), D)
			***tenemos que reequilibrar
			elseif (altura(hijoDer(D)) >= altura(hijoIzq(D))) then
				rotIzq(arbolBin(R2, eliminar(R1,I), D))
			else
				rotIzq(arbolBin(R2, eliminar(R1,I), rotDer(D)))
			fi .
		else
			if ((altura(I) - altura(eliminar(R1, D))) <= 1) then
				arbolBin(R2, I, eliminar(R1, D))
			elseif (altura(hijoIzq(I) >= altura(hijoDer(I)))) then
				rotDer(arbolBin(R2, I, eliminar(R1, D)))
			else
				rotDer(arbolBin(R2, rotIzq(I), eliminar(R1, D)))
			fi .
		fi .
***selectores
op raiz: AVLNV{X} -> X$Elt .
eq raiz(arbolBin(R, I, D)) == R .
 
op esVacio: AVL{X} -> Bool .
eq esVacio(crear) == true .
eq esVacio(arbolBin(R, I, D)) == false .
 
op altura: AVL{X} -> Nat .
eq altura(crear) == 0 .
eq altura(arbolBin(R, I, D)) == 1 + max(altura(I), altura(D)) .
 
***auxiliares
op rotDer: AVL{X} -> [AVL{X}] .
eq rotDer(arbolBin(R1, arbolBin(R2, I2, D2), D1)) ==
arbolBin(R2, I2, arbolBin(R1, D2, D)) .
 
op rotIzq: AVL{X} -> [AVL{X}] .
eq rotIzq(arbolBin(R1, I, arbolBin(R2, I2, D2))) ==
arbolBin(R2, arbolBin(R1, I, I2), D2) .
 
endfm .

Especificación completa de árbol AVL en C++:

typedef int tElemento;

typedef struct NODO_AVL {

  tElemento elemento;
  struct AVL_NODO *izqda;
  struct AVL_NODO *drcha;
  int altura;

} nodo_avl;

typedef nodo_avl *arbol_avl;

arbolAVL Crear_AVL() {

  return AVL_VACIO;

}

void Destruir_AVL (arbolAVL A) {

 if (A) {
     Destruir_AVL(A->izqda);
     Destruir_AVL(A->drcha);
     free(A);
  }

}

int miembro_AVL(tElemento e,arbolAVL A) {

  if (A == NULL)
  	 return 0;
 
  if (e == A->elemento)
  	 return 1;
  else
  	if (e < A->elemento)
   	   return miembro_AVL(e,A->izqda);
  	else
   	   return miembro_AVL(e,A->drcha);

}

void Simple_derecha(arbolAVL *A) {

  nodoAVL *p;

  p = (*A)->izqda;
  (*A)->izqda = p->drcha;
  p->drcha = (*A);
  (*A) = p;
  /* Ajustamos las alturas */
  p = (*A)->drcha;
  p->altura = maximo(altura(p->izqda),altura(p->drcha))+1;
  (*A)->altura = maximo(a1tura((*T)->izqda),altura((*T)->drcha))+1;

}

void Simple_izquierda(arbolAVL *A) {

  nodoAVL *p;

  p = (*A)->drcha;
  (*A)->drcha = p->izqda;
  p->izqda = (*A);
  (*A) = p;
  /*Ajustamos las alturas */
  p = (*A)->izqda;
  p->altura = maximo(altura(p->izqda),altura(p->drcha))+1;
  (*A)->altura = maximo(altura((*A)->izqda),altura((*A)->drcha))+1;

}

void Doble_izquierda_derecha (arbolAVL *AT) {

  simple_izquierda(&((*A)->izqda));
  simple_derecha(A);

}

void Doble_derecha_izquierda (arbolAVL *A) {

  simple_derecha(&((*A)->drcha));
  simple_izquierda(A);

}

void ajusta_AVL (tElemento e, arbolAVL *A) {

  if (!(*A))
     return;
  if (e > (*A)->elemento)
     ajusta_AVL(e,&((*A)->drcha));
  else if (e < (*A)->elemento)
          ajusta_avl(e,&((*A)->izqda));

  switch (altura((*A)->izqda)-altura((*A)->drcha)) {
  case 2:
     if (altura((*A)->izqda->izqda) > altura((*A)->izqda->drcha))
        simple_derecha(A);
     else doble_izquierda_derecha(A);
     break;
  case -2:
     if (altura((*A)->drcha->drcha) > altura((*A)->drcha->izqda))
        simple_izquierda(A);
     else doble_derecha_izquierda(A);
     break;
  default:
     (*A)->altura = maximo(altura((*A)->izqda),altura((*A)->drcha))+1;
  }

}

void insertarAVL (tElemento e, arbolAVL *A) {

  nodoAVL **p;
  
  p=T;
  while (*p!=NULL)
     if ((*p)->elemento > e)
        p = &((*p)->izqda);
     else p = &((*p)->drcha);

  (*p)=(nodo_avl *)malloc(sizeof(nodoAVL));
  if (!(*p)) 
     error("Error: Memoria insuficiente.");

  (*p)->elemento = e;
  (*p)->altura = 0;
  (*p)->izqda = NULL;
  (*p)->drcha = NULL;
  ajustaAVL(e,A);

}

void borrarAVL (tElemento e, arbolAVL *A) {

  nodoAVL **p,**aux,*dest;
  tElemento elem;

  p=A;
  elem=e;
  while ((*p)->elemento!=e) {
     elem=(*p)->elemento;
     if ((*p)->elemento > e)
        p=&((*p)->izqda);
     else p=&((*p)->drcha);
  }

  if ((*p)->izqda!=NULL && (*p)->drcha!=NULL) {
     aux=&((*p)->drcha); 
     elem=(*p)->elemento;
     while ((*aux)->izqda) { 
        elem=(*aux)->elemento;
        aux=&((*aux)->izqda);
     }
     (*p)->elemento = (*aux)->elemento;
     p=aux;
  }

if ((*p)->izqda==NULL && (*p)->drcha==NULL) {

free(*p);

(*p) = NULL;

} else if ((*p)->izqda == NULL) {

dest = (*p);

(*p) = (*p)->drcha;

free(dest);

} else {

dest = (*p);

(*p) = (*p)->izqda;

free(dest);

}

ajustaAVL(elem,A);

}

Véase también

Árbol AVL (INGLES)

Árbol Binario (INGLES)

• Árbol binario de búsqueda
• Árbol (programación)
• Árbol binario
• Árbol AVL
• Árbol rojo-negro
• Árbol splay
• Árbol multirrama