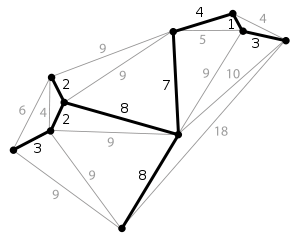
Árbol recubridor mínimo

Un ejemplo de árbol recubridor mínimo. Cada punto representa un vértice, cada arista está etiquetada con su peso, que en este caso equivale a su longitud.

Dado un grafo conexo, un árbol recubridor mínimo de ese grafo es un subgrafo que tiene que ser un árbol y contener todos los vértices del grafo inicial. Cada arista tiene asignado un peso proporcional entre ellos, que es un número representativo de algún objeto, distancia, etc.. , y se usa para asignar un peso total al árbol recubridor mínimo computando la suma de todos los pesos de las aristas del árbol en cuestión. Un árbol recubridor mínimo o un árbol expandido mínimo es un árbol recubridor que pesa menos o igual que otros árboles recubridores. Todo grafo tiene un bósque recubridor mínimo.

Un ejemplo sería una compañía de cable trazando cable a una nueva vecindad. Si está limitada a trazar el cable por ciertos caminos, entonces se hará un grafo que represente los puntos conectados por esos caminos. Algunos de estos caminos podrán ser más caros que otros, por ser más largos. Estos caminos serían representados por las aristas con mayores pesos. Un árbol recubridor para este grafo sería un subconjunto de estos caminos que no tenga ciclos pero que mantenga conectadas todas las casas. Puede haber más de un árbol recubridor posible. El árbol recubridor mínimo será el de menos coste.

En el caso de un empate, porque podría haber más de un árbol recubridor mínimo; en particular, si todos los pesos son iguales, todo árbol recubridor será mínimo. De todas formas, si cada arista tiene un peso distinto existirá sólo un árbol recubridor mínimo. La demostración de esto es trivial y se puede hacer por inducción. Esto ocurre en muchas situaciones de la realidad, como con la compañía de cable en el ejemplo anterior, donde es extraño que dos caminos tengan exactamente el mismo coste. Esto también se generaliza para los bósques recubridores.

Si los pesos son positivos, el árbol recubridor mínimo es el subgrafo de menor costo posible conectando todos los vértices, ya que los subgrafos que contienen ciclos necesariamente tienen más peso total.

Véase también

• Algoritmo de Prim
• Algoritmo de Kruskal
• Algoritmo de Dijkstra

Referencias

• Otakar Boruvka on Minimum Spanning Tree Problem (translation of the both 1926 papers, comments, history) (2000) Jaroslav Nesetril, Eva Milková, Helena Nesetrilová (section 7 gives his algorithm, which looks like a cross between Prim's and Kruskal's)
• A Minimum Spanning Tree Algorithm with Inverse-Ackermann Type Complexity, Bernard Chazelle, 1999
• [1]
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Chapter 23: Minimum Spanning Trees, pp.561–579.
• Two Algorithms for Generating Weighted Spanning Trees in Order, Harold Gabow, 1977
• State-of-the-Art Algorithms for Minimum Spanning Trees: A Tutorial Discussion, Jason Eisner, 1997

Enlaces externos

• Implementado en BGL, la "Boost Graph Library"