Algoritmo de Dijkstra

Algoritmo de Dijkstra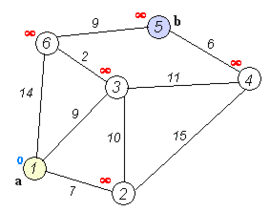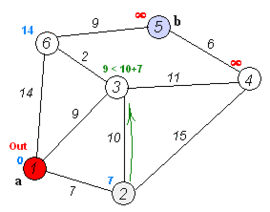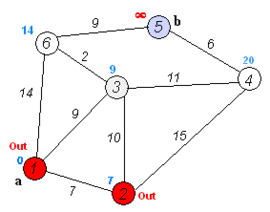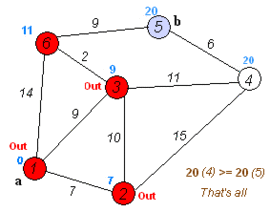
Ejecución del algoritmo de Dijkstra
Tipo	Algoritmo de búsqueda
Problema que resuelve	Problema del camino más corto
Estructura de datos	Grafo
Creador	Edsger Dijkstra
Fecha	1959
Clase de complejidad	P
Tiempo de ejecución
Peor caso

El algoritmo de Dijkstra, también llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de vértices en un grafo con pesos en cada arista. Su nombre se refiere a Edsger Dijkstra, quien lo describió por primera vez en 1959.

La idea subyacente en este algoritmo consiste en ir explorando todos los caminos más cortos que parten del vértice origen y que llevan a todos los demás vértices; cuando se obtiene el camino más corto desde el vértice origen, al resto de vértices que componen el grafo, el algoritmo se detiene. El algoritmo es una especialización de la búsqueda de costo uniforme, y como tal, no funciona en grafos con aristas de costo negativo (al elegir siempre el nodo con distancia menor, pueden quedar excluidos de la búsqueda nodos que en próximas iteraciones bajarían el costo general del camino al pasar por una arista con costo negativo).

Algoritmo

Teniendo un grafo dirigido ponderado de N nodos no aislados, sea x el nodo inicial, un vector D de tamaño N guardará al final del algoritmo las distancias desde x al resto de los nodos.

1. Inicializar todas las distancias en D con un valor infinito relativo ya que son desconocidas al principio, exceptuando la de x que se debe colocar en 0 debido a que la distancia de x a x sería 0.
2. Sea a = x (tomamos a como nodo actual).
3. Recorremos todos los nodos adyacentes de a, excepto los nodos marcados, llamaremos a estos v_i.
4. Si la distancia desde x hasta v_i guardada en D es mayor que la distancia desde x hasta a, sumada a la distancia desde a hasta v_i; esta se sustituye con la segunda nombrada, esto es:
   si (D_i > D_a + d(a, v_i)) entonces D_i = D_a + d(a, v_i)
5. Marcamos como completo el nodo a.
6. Tomamos como próximo nodo actual el de menor valor en D (puede hacerse almacenando los valores en una cola de prioridad) y volvemos al paso 3 mientras existan nodos no marcados.

Una vez terminado al algoritmo, D estará completamente lleno.

Complejidad

Orden de complejidad del algoritmo: O(|V|²+|E|) = O(|V|²) sin utilizar cola de prioridad, O((|E|+|V|) log |V|) utilizando cola de prioridad (por ejemplo un montículo).

Podemos estimar la complejidad computacional del algoritmo de Dijkstra (en términos de sumas y comparaciones). El algoritmo realiza a lo más n-1 iteraciones, ya que en cada iteración se añade un vértice al conjunto distinguido. Para estimar el número total de operaciones basta estimar el número de operaciones que se llevan a cabo en cada iteración. Podemos identificar el vértice con la menor etiqueta entre los que no están en S_k realizando n-1 comparaciones o menos. Después hacemos una suma y una comparación para actualizar la etiqueta de cada uno de los vértices que no están en S_k. Por tanto, en cada iteración se realizan a lo sumo 2(n-1) operaciones, ya que no puede haber más de n-1 etiquetas por actualizar en cada iteración. Como no se realizan más de n-1 iteraciones, cada una de las cuales supone a lo más 2(n-1) operaciones, llegamos al siguiente teorema.

TEOREMA: El Algoritmo de Dijkstra realiza O(n²) operaciones (sumas y comparaciones) para determinar la longitud del camino más corto entre dos vértices de un grafo ponderado simple, conexo y no dirigido con n vértices.

Pseudocódigo

• Estructura de datos auxiliar: Q = Estructura de datos Cola de prioridad (se puede implementar con un montículo)

   DIJKSTRA (Grafo G, nodo_fuente s)       
       para u ∈ V[G] hacer
           distancia[u] = INFINITO
           padre[u] = NULL
       distancia[s] = 0
       Encolar (cola, grafo)
       mientras que cola no es vacía hacer
           u = extraer_minimo(cola)
           para v ∈ adyacencia[u] hacer
               si distancia[v] > distancia[u] + peso (u, v) hacer
                   distancia[v] = distancia[u] + peso (u, v)
                   padre[v] = u
                   Actualizar(cola,distancia,v)

Otra versión en pseudocódigo sin cola de prioridad

función Dijkstra (Grafo G, nodo_salida s)
  //Usaremos un vector para guardar las distancias del nodo salida al resto
  entero distancia[n] //Inicializamos el vector con distancias iniciales
  booleano visto[n] //vector de boleanos para controlar los vertices de los que ya tenemos la distancia mínima
  para cada w ∈ V[G] hacer
     Si (no existe arista entre s y w) entonces
         distancia[w] = Infinito //puedes marcar la casilla con un -1 por ejemplo
     Si_no
         distancia[w] = peso (s, w)
     fin si 
  fin para
  distancia[s] = 0
  visto[s] = cierto
  //n es el número de vertices que tiene el Grafo
  mientras que (no_esten_vistos_todos) hacer 
     vertice = coger_el_minimo_del_vector distancia y que no este visto;
     visto[vertice] = cierto;
     para cada w ∈ sucesores (G, vertice) hacer
         si distancia[w]>distancia[vertice]+peso (vertice, w) entonces
            distancia[w] = distancia[vertice]+peso (vertice, w)
         fin si
     fin para
  fin mientras
fin función

Al final tenemos en el vector distancia en cada posición la distancia mínima del vertice salida a otro vertice cualquiera.

Implementación

C++

// Declaraciones en el archivo .h
int cn; //cantidad de nodos
vector< vector<int> > ady; //matriz de adyacencia
deque<int> path; // camino minimo de dijkstra
int caminosPosibles; // cantidad de caminos posibles
 
vector<int> dijkstra(int nodo, int final = 0); // el parámetro 'final' es opcional
 
// Devuelve un vector con las distancias minimas del nodo inicial al resto de los vertices.
// Guarda en path los nodos que forman el camino minimo y muestra la cantidad de caminos posibles
vector<int> Grafo :: dijkstra(int inicial, int final){
    vector<int> distancias;
    list<int> noVisitados;
    list<int> :: iterator itList;
 
    caminosPosibles = 0;
 
    //decremento para manejarme en [0, cn)
    inicial--; final--;
 
    // Seteo las distancias en infinito y marco todos los nodos como no visitados
    for(int i = 0; i < cn; i++){
        distancias.push_back(INF);
        noVisitados.push_back(i);
    }
 
    // Actual es el nodo inicial y la distancia a si mismo es 0
    int actual = inicial;
    distancias[inicial] = 0;
 
    // Inicializo el camino minimo en infinito.
    path = deque<int>(cn, INF);
 
    while(!noVisitados.empty()){
        // Para cada nodo no visitado, calculo la distancia tentativa al nodo actual;
        // si es menor que la distancia seteada, la sobreescribo.
        for(itList = noVisitados.begin(); itList != noVisitados.end(); itList++){
            // distancia tentativa = distancia del inicial al actual + distancia del actual al noVisitado
            int dt = distancias[actual] + ady[actual][*itList];
            if(distancias[*itList] > dt){
                distancias[*itList] = dt;
 
                // Agrego a camino el nodo (actual) a traves del cual el nodo inicial se conecta con *itList
                path[*itList] = actual;
            }
            else if(distancias[*itList] == dt && *itList == final)
                caminosPosibles++;
 
        }
        // Marco como visitado el nodo actual, la distancia seteada es la minima.
        noVisitados.remove(actual);
 
        // Si no lo pase como parametro final vale -1, en ese caso el if nunca da true.
        if(actual == final) break;
 
        // El nodo actual ahora es el nodo no visitado que tiene la menor distancia al nodo inicial.
        int min = INF;
        for(itList = noVisitados.begin(); itList != noVisitados.end(); itList++)
            if(min >= distancias[*itList]){
                min = distancias[*itList];
                actual = *itList;
            }
    }
 
    // Si final vino como parámetro obtengo el camino minimo y lo guardo en path
    if(final != -1){
        deque<int> temp;
        int nodo = final;
 
        while(nodo != inicial){
            temp.push_front(nodo);
            nodo = path[nodo];
        }
 
        path = temp;
 
        if(ady[inicial][final] != INF)
            caminosPosibles++;
 
        cout << "Caminos Posibles " << caminosPosibles << endl;
    }    
    return distancias;
}

Enlaces externos

• Wikimedia Commons alberga contenido multimedia sobre Algoritmo de DijkstraCommons.
• Presentación del Algoritmo de Dijkstra
• Applets en Java para probar el algoritmo de Dijkstra (Inglés)
• Graph módulo Perl en CPAN
• Bio::Coordinate::Graph módulo Perl en CPAN que implementa el algoritmo de Dijkstra
• Video Tutorial en VideoPractico.com de Dijkstra
• giswiki.net Algoritmo de Dijkstra en lenguajes como PHP, Actionscript y otros