- Arco capaz
-
Arco capaz
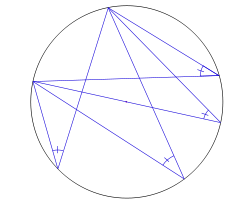
El arco capaz es el lugar geométrico de los puntos del plano desde los que se ve un segmento bajo un ángulo determinado; es decir, el lugar geométrico de los vértices de los ángulos que tienen el mismo valor y abarcan un mismo segmento.
El arco capaz de un segmento AB, de ángulo λ, es un arco de circunferencia que contiene el vértice del ángulo λ, y los puntos A y B.
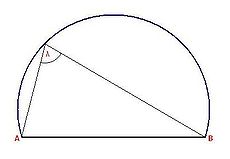
El caso más notorio es el arco capaz del diámetro de una circunferencia, de ángulo λ = 90º, siendo la misma circunferencia el lugar donde se encuentran todos los vértices de los ángulos que miden 90º, cuyos lados contienen los extremos del diámetro.
Es muy útil en dibujo geométrico para resolver problemas de polígonos y ángulos.
Construcción
Para construir el arco capaz, de ángulo λ, del segmento AB:
- Primer método
- se trazan dos mediatrices del triángulo definido por los extremos del segmento AB y el vértice del ángulo λ.
- Dichas mediatrices se cortan en el punto O, que es el centro del arco capaz buscado.
- Bastará con dibujar con el compás un arco de centro O y radio OA.
El punto O es el circuncentro: el centro de la circunferencia circunscrita, que equidista del vértice, y de los puntos A y B.
- Segundo método
- se traza la mediatriz m de dicho segmento;
- se trazará una recta r que forme un ángulo λ con el segmento AB, con vértice en A;
- desde A, se dibujará una recta s perpendicular a la recta r.
- El punto de corte O entre la recta s y la mediatriz m es el centro del arco capaz buscado.
- Bastará con dibujar con el compás un arco de centro O y radio OA.
- Características
Por semejanza de triángulos, se deduce que:
- el ángulo formado por la recta s y la mediatriz m mide igual que el ángulo λ;
- por tanto, el ángulo con centro en O, conformado por la recta s y la recta simétrica a s, respecto de la mediatriz m, medirá el doble que el ángulo λ, es decir, AOB medirá 2λ.
Enlaces externos
Categorías: Curvas | Ángulos
Wikimedia foundation. 2010.