- Rombicosidodecaedro
-
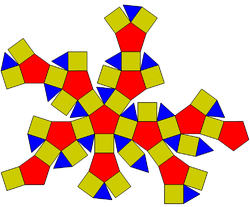
Rombicosidodecaedro
Rombicosidodecaedro Imagen 
Grupo Sólidos de Arquímedes Número de caras 62 Polígonos que forman las caras 20 Triángulos equiláteros
30 Cuadrados
12Pentágonos EquiláterosNúmero de aristas 120 Número de vértices 60 Tipo de Vértice Uniforme de Orden 4 Caras relacionadas en los vértices 2 cuadrados
1 Triángulo
1 PentágonoSimetría Icosaédrica (Ih) Poliedro dual Hexecontaedro deltoidal Propiedades Poliedro convexo, de vértices uniformes El Rombicosidodecaedro es un sólido de Arquímedes, que sin inflar puede llenar hasta el 93.32% de una esfera. Está formado por 12 pentágonos, 30 cuadrados y 20 triángulos,60 vértices y 120 aristas; 62 caras en total.
Este sólido se obtiene:
Como dual del Hexecontaedro deltoidal o por expansión del Octaedro.
El Rombicosidodecaedro conocido se refiere al hecho de que las 30 caras cuadradas yacen en los mismos planos que las 30 caras del Triacontaedro rómbico que es dual al icosidodecaedro. También puede ser llamado un dodecaedro truncado o Icosaedro truncado mediante operaciones de truncamiento del poliedro uniforme.
Contenido
Relaciones geométricas
Si se sopla un icosahedron moviendo las caras lejos del origen en forma correcta, sin cambiar la orientación o el tamaño de las caras, y se hace lo mismo a su dodecaedro dual, luego si parcha las perforaciones rectangulares del resultado, usted consigue un rombicosidodecaedro. Por lo tanto, tiene el mismo número de triángulos que un icosaedro y el mismo número de pentágonos que un dodecaedro, con un cuadrado para cada borde.
Coordenadas cartesianas
Coordenadas cartesianas para los vertices de un rombicosidodecaedro centrado en el origen son
- (±1, ±1, ±τ3),
- (±τ3, ±1, ±1),
- (±1, ±τ3, ±1),
- (±τ2, ±τ, ±2τ),
- (±2τ, ±τ2, ±τ),
- (±τ, ±2τ, ±τ2),
- (±(2+τ), 0, ±τ2),
- (±τ2, ±(2+τ), 0),
- (0, ±τ2, ±(2+τ)),
donde τ = (1+√5)/2 es el número áureo.
Planificación
Area y Volumen
Area y volumen de un Rombicosidodecaedro de lado a:
Areas de interés
El Rombicosidodecaedro sería un excelente modelo geométrico para la hechura de pelotas de fútbol, pero seria muy costoso su uso, por eso el balón tradicional es como un Icosaedro truncado.
Categoría: Sólidos arquimedianos
Wikimedia foundation. 2010.

![\begin{align}
A & = \left \{ 30 + \sqrt{ 30 \left [ 10 + 3\sqrt{5} + \sqrt{15 (5 + 2\sqrt{5})} \right ] } \right \} a^2 \\
& \approx 59.3059828a^2 \\
V & = \frac{1}{3} (60+29\sqrt{5})a^3 \approx 41.6153238a^3 \\
\end{align}](/pictures/eswiki/101/e89e06c3c9735cd479857c2ba62d17fd.png)