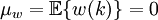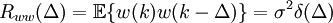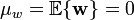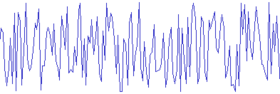
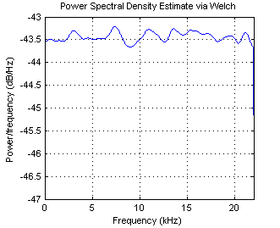
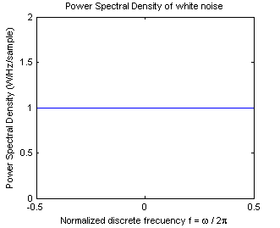
El ruido blanco es una señal aleatoria (proceso estocástico) que se caracteriza porque sus valores de señal en dos instantes de tiempo diferentes no guardan correlación estadística. Como consecuencia de ello, su densidad espectral de potencia (PSD, Power Spectral Density) es una constante, i.e, su gráfica es plana.^[1] Esto significa que la señal contiene todas las frecuencias y todas ellas tienen la misma potencia. Igual fenómeno ocurre con la luz blanca, lo que motiva la denominación.

Si la PSD no es plana entonces se dice que el ruido está "coloreado" (correlacionado). Dependiendo de la forma que tenga la gráfica de la PSD del ruido se definen diferentes colores

Contenido 1 Ejemplos 2 Definición matemática 3 Análisis y síntesis de procesos estocásticos WSS coloreados 4 Aplicaciones 4.1 Procesamiento de señal 4.2 Generación de números aleatorios 4.3 Uso en vehículos de emergencia 4.4 Uso en personas 5 Referencias 6 Véase también

Ejemplos

Ejemplo de ruido blanco ¡Precaución! Se sugiere escuchar a un nivel bajo de volumen para evitar daños auditivos y en el sistema de amplificación ¿Problemas al escuchar este archivo? Vea Ayuda:Multimedia.

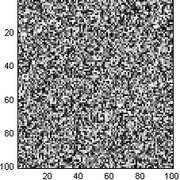
Esta imagen en B/N también^[2] es ruido blanco, sus píxeles no guardan correlación entre sí y por tanto su densidad espectral de potencia es constante. Si la imagen fuese en color, entonces la "nieve" sería de colores aleatorios.

Esta es la típica imagen que se ve en la pantalla de un televisor analógico cuando no está sintonizado en ningún canal. La señal que recibe entonces el demodulador puede considerarse como ruido blanco, ya que es el resultado de sumar el ruido electromagnético del canal radio más el que generan los propios circuitos electrónicos del televisor, múltiples interferencias de baja intensidad todas ellas independientes entre sí, etc. En este último caso, la "nieve" no permanecería estática sino que cambiaría constantemente con el tiempo porque la señal de televisión es una señal de video, i.e, una sucesión de imágenes (25 fotogramas/s)

Definición matemática

El ruido blanco es un caso particular de proceso estocástico WSS en el que las variables aleatorias que lo forman no están correlacionadas. Es decir, si se tiene un proceso estocástico w(k) WSS (lo supodremos de tiempo discreto y real, equivalentemente para procesos de tiempo continuo), debe ocurrir que

Si en lugar de tener la distribución de probabilidad del proceso lo que tenemos es una realización temporal del mismo en forma de vector columna (lo más usual), entonces las ecuaciones anteriores se expresan normalmente en forma matricial

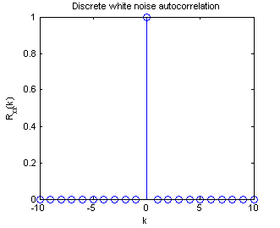
Como el proceso no está correlacionado, su función de autocorrelación es una delta y su densidad espectral de potencia (PSD, Power Spectral Density) S_xx(f) es una constante

S_xx(f) = TF{R_ww(Δ)} = TF{σ²δ(Δ)} = σ²

Como la PSD es constante, la señal no está limitada en banda y su potencia es -teóricamente- infinita. En la práctica, se considera que una señal es blanca si su PSD es constante en la banda de frecuencia de interés en la aplicación. Por ejemplo: si se trata de una aplicación de audio, el ruido será blanco si su espectro es plano entre 20Hz y 20KHz que es la banda de frecuencia audible por el oído humano.

En cualquier proceso estocástico existen siempre dos componentes:

• Una componente innovadora, que no se puede predecir mediante predicción lineal y que representa la entropía, la incertidumbre, el caos, lo que no se puede predecir de ninguna manera
• Una componente redundante que es posible predecir y, por tanto, eliminar. En esto se basan las técnicas de compresión sin pérdidas de la señal como, por ejemplo, ADPCM o más específicamente para señales de voz la norma G.721

La PSD es la transformada de Fourier de la función de autocorrelación, y como esta es una transformación matemática unívoca, se ve que la función de autocorrelación y la PSD contienen básicamente la misma información acerca de una señal. Son dos formas distintas de ver lo mismo: el grado de entropía de una señal. La entropía de una señal en este caso puede verse como una medida de lo plano que es su espectro. Una señal cuyo espectro no sea plano se dice que está "coloreada" (autocorrelacionada o que tiene redundancia).

El ruido blanco es un proceso completamente innovador, caótico, no tiene redundancia y por tanto no se puede comprimir.

Análisis y síntesis de procesos estocásticos WSS coloreados

También se puede ver el ruido blanco como el residuo que queda después de extraer toda la redundancia a un proceso estocástico WSS coloreado. De hecho, es posible demostrar que todo proceso estocástico estacionario en sentido amplio (WSS, Wide-Sense Stationarity) se puede obtener filtrando ruido blanco con un filtro todo polos (modelo AR), con un filtro todo ceros (modelo MA) o con un filtro de polos y ceros (modelo ARMA).

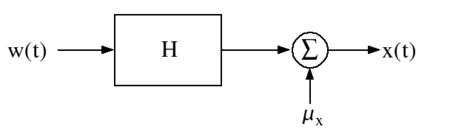
En el siguiente diagrama se filtra ruido blanco w(t) mediante el filtro lineal H, obteniendo a la salida el proceso x(t) coloreado (el filtro H introduce correlación entre las muestras del proceso w(t))

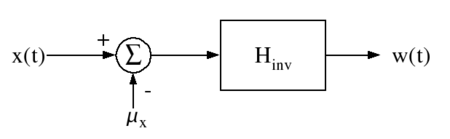
Haciendo predicción lineal sobre x(t) se obtiene el filtro H ^{− 1} que es el filtro inverso (filtro de deconvolución) de H y que permite, después de ajustar las medias de los procesos, obtener de nuevo el proceso de ruido blanco original w(t).

Estas técnicas tienen gran importancia en procesado de la señal. En filtrado adaptativo se usan para estudiar la estabilidad de algoritmos adaptativos para filtros IIR. En codificación de voz, el códec vocoder en ningún momento transmite las muestras de la señal sino un bit que decide si el fonema es sordo/sonoro y a continuación los parámetros del modelo de predicción lineal para cada caso (filtro H ^{− 1} del diagrama). Con esta técnica se consigue codificar la voz con tasas tan bajas como 2,4 kbps y con una calidad suficientemente inteligible.

Aplicaciones

Procesamiento de señal

En general, el ruido blanco tiene muchas aplicaciones en procesado de señal:

• Sirve para determinar la función de transferencia de cualquier sistema lineal e invariante con el tiempo (LTI, Linear Time Invariant). Por ejemplo, en acústica arquitectónica la función de transferencia se usa para medir el aislamiento acústico y la reverberación de la sala
• En síntesis de audio (música electrónica) se usa para sintetizar el sonido de instrumentos de percusión, o los fonemas sordos /s/ /t/ /f/ etc
• También se puede usar para mejorar las propiedades de convergencia de ciertos algoritmos de filtrado adaptativo mediante la inyección de una pequeña señal de ruido blanco en algún punto del sistema.

Generación de números aleatorios

El ruido blanco generado por ciertos procesos físicos naturales o artificiales se usa como base para la generación de números aleatorios de calidad puesto que es, como ya se ha dicho, una fuente de entropía.

Uso en vehículos de emergencia

Algunos vehículos de emergencia lo usan debido a que es fácil distinguirlo del ruido de fondo y no queda enmascarado por el eco, por lo que es más fácil su localización espacial

Uso en personas

Puede ser usado para desorientar a personas antes de un interrogatorio y como técnica de privación sensorial. Por otra parte, el ruido blanco de baja intensidad puede favorecer la relajación y el sueño. En tiendas especializadas e internet pueden adquirirse CDs con largas secuencias de ruido blanco, así como aparatos electromecánicos que hacen uso del principio del ruido blanco para "enmascarar" los ruidos repentinos y molestos.

Referencias

Véase también

• Proceso estocástico
• Densidad espectral de potencia
• Correlación
• Autocorrelación
• Covarianza
• Matriz de correlación
• Ruido rosa
• Ruido marrón
• Ruido de color
• Filtro adaptativo
• Espectro de frecuencia
• Predicción lineal
• Modelo ARMA