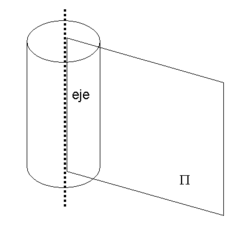
Simetría axial

Simetría axial
Para los seres vivos, véase Simetría radial (biología).
Problema axisimétrico respecto a un eje, la situación en todos los semiplanos Π, como el de la figura es idéntica.

La simetría axial (también llamada rotacional, radial o cilíndrica) es la simetría alrededor de un eje, de modo que un sistema tiene simetría axial o axisimetría cuando todos los semiplanos tomados a partir de cierto eje y conteniéndolo presentan idénticas características.

Dada una recta \scriptstyle e se llama simetría axial de eje e al movimiento que transforma a un punto P en otro punto P' verificando que:

  • El segmento PP' es perpendicular a \scriptstyle e.
  • Los puntos P y P' equidistan del eje \scriptstyle e.

Dicho de otra forma el eje \scriptstyle e es la mediatriz del segmento PP'

La simetría axial no solo se presenta entre un objeto y su reflexión, pues muchas figuras que mediante una línea pueden partirse en dos secciones que son simétricas con respecto a la línea. Estos objetos tienen uno (o más) ejes de simetría.

La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como referencia una línea que se conoce con el nombre de eje de simetría. En la simetría axial se da el mismo fenómeno que en una imagen reflejada en el espejo.

A los puntos que pertenecen a la figura simétrica se les llama puntos homólogos, es decir, A’ es homólogo de A, B’ es homólogo de B, y C’ es homólogo de C. Además, las distancias existentes entre los puntos de la figura original son iguales que las distancias entre los puntos de la figura simétrica. En este caso: La simetría axial se puede dar también en un objeto con respecto de uno o más ejes de simetría.

Si se doblara la figura sobre el eje de simetría trazado, se podría observar con toda claridad que los puntos de las partes opuestas coinciden, es decir, ambas partes son congruentes.

Contenido

Física

Un cierto número de problemas físicos de interés, especialmente relacionados con la teoría de campos, los medios continuos o la teoría cuántica son más fáciles de resolver cuando los datos de partida tiene simétría axial, ya que la solución para ciertas magnitudes incógnitas también tendrá simetría axial. Eso permite reducir un problema con tres coordenadas espaciales a un problema de dos variables. Por ejemplo en varias áreas de la resolución de ciertos problemas requiere estudiar la ecuación de Poisson siguiente:

\frac{\partial^2 \varphi}{\partial x^2} + \frac{\partial^2 \varphi}{\partial y^2} + \frac{\partial^2 \varphi}{\partial z^2} = \rho(\mathbf{x})

Cuando la función "fuente" tiene simetría axial, es decir:

\rho(x,y,z) = \rho(x\cos\alpha-y\sin\alpha, y\cos\alpha+x\sin\alpha, z)\,

El problema puede reformularse en términos de dos variables como:

\frac{\partial^2 \tilde\varphi}{\partial r^2} + \frac{1}{r}\frac{\part \tilde\varphi}{\part r} + \frac{\part^2 \tilde\varphi}{\part z^2} = \tilde\rho(r,z)

Donde:

\begin{cases} \rho(x,y,z) = \tilde\rho(\sqrt{x^2+y^2},z), & \tilde\rho(r,z) = \rho(r\cos\theta,r\sin\theta,z) \\ \varphi(x,y,z) = \tilde\varphi(\sqrt{x^2+y^2},z), & \tilde\varphi(r,z) = \varphi(r\cos\theta,r\sin\theta,z) \end{cases}

Teoría de grupos

Dado un problema geométrico o físico caracterizado por un cierto número de magnitudes escalares \phi(\mathbf{x}) o propiedades tensoriales T(\mathbf{x})\in \mathcal{T}^p_q(\R^n) se dice que el problema tiene simetría axial si existen representaciones Fp,q del grupo SO(2):[1]

F_{p,q}:SO(2)\to \mathcal{T}^p_q(\R^n)\otimes {\mathcal{T}^p_q}^*(\R^n)

Tales que:

[F_{p,q}(\mathbf{T})](F_{1,0}(\mathbf{x})) = \mathbf{T}(\mathbf{x}), \quad \phi(F_{1,0}(\mathbf{x})) = \phi(\mathbf{x})

Esta última expresa la condición de que el hecho de rotar el sistema de ejes deja forminvariantes las cantidades básicas que caracterizan el problema.

Véase también

Referencia

Notas

  1. ↑ Galindo y Pascual, pp. 239-250.

Bibliografía


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Simetría axial — Se llama simetría axial a la simetría alrededor de un eje, de modo que un sistema tiene simetría axial o axisimetría cuando al cortar dicho sistema por un semiplano que contiene al eje el resultado es siempre el mismo. «Dada una recta e se llama… …   Enciclopedia Universal

  • axial — adjetivo 1. Del eje: plano axial, simetría axial …   Diccionario Salamanca de la Lengua Española

  • Simetría — El hombre Vitrubio, de Leonardo da Vinci (ca. 1487), es una representación frecuente de la simetría del cuerpo humano, y por extensión del mundo natural. La simetría es un rasgo característico de formas geométricas, sistemas, ecuaciones y otros… …   Wikipedia Español

  • Simetría — (Del gr. symmetria < syn , conjuntamente + metron, medida.) ► sustantivo femenino 1 Modo de estar colocadas las cosas de un conjunto, de tal forma que existen dos partes exactamente iguales, que se contraponen. ANTÓNIMO asimetría 2 BOTÁNICA,… …   Enciclopedia Universal

  • Simetría radial (biología) — Una medusa, animal típicamente radial. La simetría radial es la simetría definida por un eje heteropolar (distinto en sus dos extremos). El extremo que contiene la boca se llama lado oral, y su opuesto lado aboral o abactinal. Sobre este eje, se… …   Wikipedia Español

  • Simetría esférica — La simetría esférica es la simetría respecto a un punto central, de modo que un sistema físico o geométrico tiene simetría esférica cuando todos los puntos a una cierta distancia del punto central son equivalentes. Contenido 1 Física 2 Teoría de… …   Wikipedia Español

  • axial — {{＃}}{{LM A04280}}{{〓}} {{［}}axial{{］}} ‹a·xial› {{《}}▍ adj.inv.{{》}} Del eje o relacionado con él: • Una figura plana tiene simetría axial si existe una línea llamada eje que la divide en dos mitades simétricas.{{○}} {{★}}{{＼}}ETIMOLOGÍA:{{／}}… …   Diccionario de uso del español actual con sinónimos y antónimos

  • Transformación isométrica — Saltar a navegación, búsqueda La imajen de un objeto reflejada en un espejo plano, es un ejemplo de transformación isométrica: la simetría. Las transformaciones isométricas son transformaciones de figuras en el plano que se realizan sin variar… …   Wikipedia Español

  • Isometría afín — La imagen de un objeto reflejado en un espejo plano, es un ejemplo de transformación isométrica: la simetría. Las transformaciones isométricas son transformaciones de figuras en el plano que se realizan sin variar las dimensiones ni el área de… …   Wikipedia Español

  • Pentominó — Saltar a navegación, búsqueda Un pentominó (Griego πέντε / pente) es una poliforma de la clase poliominó que consiste en una figura geométrica compuesta por cinco cuadrados unidos por sus lados. Existen doce pentominós diferentes, que se nombran… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”