Isometría afín

La imagen de un objeto reflejado en un espejo plano, es un ejemplo de transformación isométrica: la simetría.

Las transformaciones isométricas son transformaciones de figuras en el plano que se realizan sin variar las dimensiones ni el área de las mismas; la figura inicial y la final son semejantes, y geométricamente congruentes.

La palabra isometría tiene su origen en el griego iso (igual o mismo) y metria (medir), una definición cercana es igual medida. Existen tres tipos de isometrías: traslación, simetría y rotación.

Traslación

La traslación es una isometría que realiza un cambio de posición, es el cambio de lugar, determinada por un vector.

Traslación del punto A a su imagen A' según el vector AA'

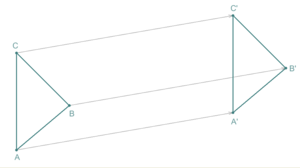Traslación de un triángulo.

Se llama traslación de vector a la isometría que a cada punto m del plano le hace corresponder un punto m' del mismo plano tal que mm' es igual a v.

Las traslaciones están marcadas por tres elementos: La dirección, si es horizontal, vertical un oblicua. El sentido, derecha, izquierda, arriba y abajo. Y la magnitud del desplazamiento que se refiere a cuanto se desplazó la figura en una unidad de medida.s Esto hace referencia exclusivamente a las traslaciones isometricas

Simetría

Simetría es la correspondencia exacta en la disposición regular de las partes o puntos de un cuerpo o figura con relación a un punto (centro), una recta (eje) o un plano. Se denominan: central, axial y especular o bilateral.

Simetría central

La simetría central, en geometría, es una transformación en la que a cada punto se le asocia otro punto, que debe cumplir las siguientes condiciones:

a) El punto y su imagen estén a igual distancia de un punto llamado centro de simetría.

b) El punto, su imagen y el centro de simetría pertenezcan a una misma recta.

Simetría central del punto A.

Simetría central del triángulo ABC, respecto del punto O.

Según estas definiciones, con una simetría central se obtiene la misma figura con una rotación de 180 grados.

Simetría axial

La simetría axial, en geometría, es una transformación respecto de un eje de simetría, en la cual, a cada punto de una figura se asocia a otro punto llamado imagen, que cumple con las siguientes condiciones:

a) La distancia de un punto y su imagen al eje de simetría, es la misma.

b) El segmento que une un punto con su imagen, es perpendicular al eje de simetría.

Simetría axial del punto A.

Simetría axial de un triángulo.

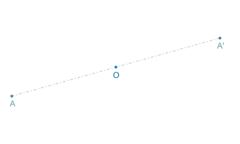
En la simetría axial se conservan las distancias pero no el sentido de los ángulos. El eje de simetría es la mediatriz del segmento AA'.

Composición de simetrías

Si se aplica la misma simetría dos veces, se obtiene una identidad.

Si se aplican dos simetrías respecto de ejes paralelos, se obtiene una traslación cuyo desplazamiento es el doble de la distancia entre dichos ejes.

Si se aplican dos simetrías respecto de ejes que se cortan en O, se obtiene giro con centro en O, cuyo ángulo es el doble del que forman dichos ejes.

Rotación

Una rotación, en geometría, es un movimiento de cambio de orientación de un cuerpo, de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante de un punto fijo, y tiene las siguientes características:

• Un punto denominado centro de rotación.
• Un ángulo
• Un sentido de rotación.

estas transformaciones pueden ser positivas o negativas dependiendo del sentido de giro. Para el primer caso debe ser un giro en sentido contrario a las manecillas del reloj, y será negativo el giro cuando sea en sentido de las manecillas.

Rotación del punto A, respecto del punto O.

Enlaces externos

• Simetrías, en Descartes.cnice.mec.es
• Simetrías, en isftic.mepsyd.es
• Función simétrica, en Descartes.cnice.mec.es