Superficie reglada

Superficie reglada

Una superficie reglada, en geometría, es la generada por una recta, denominada generatriz, al desplazarse sobre una curva o varias, denominadas directrices. En función de las características y condiciones particulares de estos elementos, recibe diversos nombres.

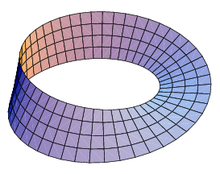Plot paramétrico de una banda de Möbius.

Clasificación de las superficies regladas

Superficies regladas son:

  • el plano
  • las superficies de curvatura simple:
    • superficie cilíndrica
      • superficie cilíndrica de revolución
      • superficie cilíndrica de no revolución
    • superficie cónica
      • superficie cónica de revolución
      • superficie cónica de no revolución
  • las superficies alabeadas
    • cilindroide
    • conoide
    • superficie doblemente reglada
      • paraboloide hiperbólico
      • hiperboloide de revolución

Ecuaciones matemáticas

Un hiperboloide de una sola hoja, es una superficie de revolución. Los alambres son líneas rectas.

Una superficie \mathbf{S} es reglada si por cada punto de la misma, existe una línea recta contenida en \mathbf{S}. Una superficie reglada \, S puede ser siempre descrita (al menos localmente) por una ecuación paramétrica de la siguiente forma:

\mathbf{S}(t,u) = \mathbf{p}(t) + u \mathbf{r}(t)

donde \mathbf{p}(t) es una curva en \mathbf{S}, y \mathbf{r}(t) es una curva en la esfera unidad. Así, por ejemplo,

\begin{align} \mathbf{p} &= (\cos(t), \sin(t), 0)\\ \mathbf{r} &= \left( \cos \left( \frac{t}{2} \right) \cos(t) , \cos \left( \frac{t}{2} \right) \sin(t), \sin \left( \frac{t}{2} \right) \right) \end{align}

obtenemos una superficie que contiene la Cinta de Möbius.

Alternativamente, una superficie reglada \mathbf{S} puede ser modelada paramétricamente como:

\mathbf{S}(t,u) = (1-u) \mathbf{p}(t) + u \mathbf{q}(t)

Donde \mathbf{p} y \mathbf{q} son dos curvas de \mathbf{S} que no se intersecan. Por ejemplo, cuando \mathbf{p}(t) y \mathbf{q}(t) se mueven con velocidad constante a lo largo de dos rectas alabeadas, la superficie es un paraboloide hiperbólico, o parte de un hiperboloide de una sola hoja.

x^2 + y^2 - z^2 = 1 \,

Superficies desarrollables

Una banda de Möbius.

Un caso especial de la superficies regladas son las superficies desarrollables que, mediante deformaciones que no alteren las distancias entre sus puntos, pueden ser transformadas en un fragmento plano. Técnicamente existe una isometría entre estas superficies y un fragmento de plano. Decimos que es localmente desarrollable si existen isometrías locales; para que esto ocurra es necesario y suficiente que la curvatura gaussiana sea nula.

El cono, el cilindro y el propio plano son desarrollables, mientras que el hiperboloide no lo es. Para que una superficie sea desarrollable, es condición necesaria y suficiente que pueda ser construida con un trozo de papel sin arrugarlo, dicho coloquialmente. Así, una superficie construida plegando un pedazo rectangular de papel será desarrollable como una banda de Möbius o un cilindro. Una condición necesaria, tal como se desprende del theorema egregium de Gauss, es que la curvatura gaussiana de la superficie reglada sea idénticamente nula.


Wikimedia foundation. 2010.

Игры ⚽ Поможем написать курсовую

Mira otros diccionarios:

  • superficie reglada — f Superficie que se engendra al desplazar una lнnea recta …   Diccionario de Construcción y Arquitectur

  • superficie reglada — ► locución GEOMETRÍA Aquella sobre la cual se puede aplicar una regla en una o en más direcciones …   Enciclopedia Universal

  • superficie — (Del lat. superficĭes). 1. f. Límite o término de un cuerpo, que lo separa y distingue de lo que no es él. 2. Extensión de tierra. 3. Aspecto externo de algo. 4. Fís. Magnitud que expresa la extensión de un cuerpo en dos dimensiones, largo y… …   Diccionario de la lengua española

  • Superficie — (Del lat. superficies.) ► sustantivo femenino 1 Límite exterior de un cuerpo, que delimita el espacio que ocupa y lo separa y distingue del espacio circundante: ■ toda la superficie de su propiedad está cercada. SINÓNIMO extensión 2 Extensión de… …   Enciclopedia Universal

  • Superficie (matemática) — Para otros usos de este término, véase superficie (desambiguación). Ilustración de una superficie curvada, inmersa en , orientable y con borde; sobre la que se ha dibujado un conjunto de líneas coordenadas ortogonales. Una superficie es de hecho… …   Wikipedia Español

  • Superficie — El término superficie puede designar: En geografía: a la extensión o área de un territorio. En matemática: superficie, es aquello que sólo tiene longitud y anchura. –Euclides, Los Elementos, Libro I, definición 5ª. superficies curvas: superficie… …   Wikipedia Español

  • superficie alabeada — ► locución GEOMETRÍA La reglada que no es desarrollable …   Enciclopedia Universal

  • superficie desarrollable — ► locución GEOMETRÍA La reglada que puede extenderse sobre un plano, como la cilíndrica o la cónica …   Enciclopedia Universal

  • Cilindro — Para otros usos de este término, véase Cilindro (desambiguación). Un cilindro circular recto. Un cilindro, en geometría, es la superficie formada por los puntos situados a una distancia fija de una línea recta dada, el eje del cilindro. Como… …   Wikipedia Español

  • Cono (geometría) — Para otros usos de este término, véase cono. En geometría, un cono recto es un sólido de revolución generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos. Al círculo conformado por el otro cateto se denomina base y al… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”