- Banda de Möbius
-
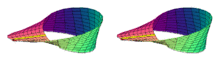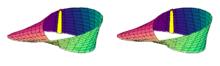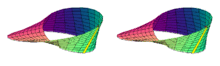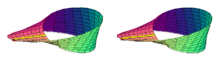
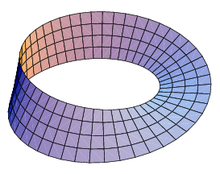
La banda de Möbius o cinta de Möbius (pronunciado /ˈmøbiʊs/ o en español a menudo «moebius») es una superficie con una sola cara y un solo borde. Tiene la propiedad matemática de ser un objeto no orientable. También es una superficie reglada. Fue co-descubierta en forma independiente por los matemáticos alemanes August Ferdinand Möbius y Johann Benedict Listing en 1858.
Banda de Moebius conformada con una cinta de papel, cuyos extremos se han unido girándolos.
Contenido
Construcción de una cinta de Möbius
Para construirla, se toma una cinta de papel y se pegan los extremos dando media vuelta a uno de ellos.
Se parte de una cinta cerrada de dos componentes en la frontera (un cilindro
), se hace un corte (entre las dos fronteras), se gira 180° uno de los extremos y se vuelve a pegar.Propiedades
La banda de Möbius posee las siguientes propiedades:
Banda de Möbius.
Plot paramétrico de una banda de Möbius.- Tiene sólo una cara:
Si se colorea la superficie de una cinta de Möbius, comenzando por la «aparentemente» cara exterior, al final queda coloreada toda la cinta, por tanto, sólo tiene una cara y no tiene sentido hablar de cara interior y cara exterior (véase en la imagen).
- Tiene sólo un borde:
Se puede comprobar siguiendo el borde con un dedo, apreciando que se alcanza el punto de partida habiendo recorrido "ambos" bordes; por tanto, sólo tiene un borde.
- Esta superficie no es orientable:
Una persona que se desliza «tumbada» sobre una banda de Möbius, mirando hacia la derecha, al dar una vuelta completa aparecerá mirando hacia la izquierda. Si se parte con una pareja de ejes perpendiculares orientados, al desplazarse paralelamente a lo largo de la cinta, se llegará al punto de partida con la orientación invertida.
- Otras propiedades:
Si se corta una cinta de Möbius a lo largo, se obtienen dos resultados diferentes, según dónde se efectúe el corte. Si el corte se realiza en la mitad exacta del ancho de la cinta, se obtiene una banda más larga pero con dos vueltas; y si a esta banda se la vuelve a cortar a lo largo por el centro de su ancho, se obtienen otras dos bandas entrelazadas pero con vueltas. A medida que se van cortando a lo largo de cada una, se siguen obteniendo más bandas entrelazadas.[1] Si el corte no se realiza en la mitad exacta del ancho de la cinta sino a cualquier otra distancia fija del borde, entonces se obtienen dos cintas entrelazadas diferentes: una idéntica a la original pero más angosta y la otra con el doble de longitud y una vuelta completa.
Este objeto se utiliza frecuentemente como ejemplo en topología.
Geometría
Una forma de representar la banda de Möbius (cerrada y con frontera) como un subconjunto de
es mediante la parametrización:![\begin{cases}
x(u,v)=\left[1+\cfrac{v}{2}\cos\cfrac{u}{2}\right]\cos(u)\\
y(u,v)=\left[1+\cfrac{v}{2}\cos\cfrac{u}{2}\right]\sin(u)\\
z(u,v)=\frac{v}{2}\sin\cfrac{u}{2} \end{cases}](9/9c9e8f26d7c38fa75b5ee395a64283a4.png)
donde
y 
.Representa una banda de Möbius de ancho unitario, cuya circunferencia central tiene radio unitario y se encuentra en el plano coordenado x-y centrada en
. El parámetro u recorre la banda longitudinalmente, mientras v se desplaza de un punto a otro del borde, cruzando transversalmente la circunferencia central.Con la parametrización anterior podemos obtener su curvatura gaussiana la cual es:
En coordenadas cilíndricas
, se puede representar una versión sin frontera (abierta) de la banda de Möbius mediante la ecuación:
Topología
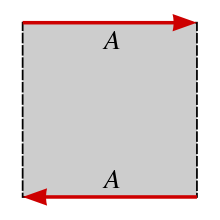
Topológicamente, la banda de Möbius puede definirse como el cuadrado
![\scriptstyle[0,1] \times [0,1]](e/73e80ab91ce1e439d855abdc829e3c8e.png)
que tiene sus aristas superior e inferior identificadas (topología cociente) por la relación 
para 
, como en el diagrama que se muestra en la figura de la derecha.
Para transformar un cuadrado en una banda de Möbius, unir las aristas etiquetadas con A de manera tal que las direcciones en que las flechas apuntan sea la misma.La banda de Möbius es una variedad bidimensional (es decir, una superficie). Es un ejemplo estándar de una superficie no orientable. La banda de Möbius es un ejemplo elemental -también- para ilustrar el concepto matemático de fibrado topológico.
Precisamente, como objeto topológico, la banda de Möbius también es considerada como el espacio total
de un fibrado no trivial teniendo como base la 1-esfera 
y fibra un intervalo, i.e.-
- <mathI-fibrados sobre la circunferencia.
Objetos relacionados
Análoga a la banda de Möbius es la botella de Klein, pues también tiene sólo una superficie, donde no se puede diferenciar «fuera» de «dentro».
Esto último significa que mientras la banda se encaja (embedding) en
, la botella no.La banda de Möbius en el arte
Pintura mural.El 17 de octubre de 1996, se estrenó la película Moebius,[2] [3] realizada en Argentina. Dicha película hace referencia a la teoría de la cinta que lleva el mismo nombre, aplicada a una supuesta red de subterráneos de la Ciudad de Buenos Aires ampliada. Se basa en un cuento de A. J. Deutsch, A Subway Named Moebius (1950).
Johan Sebastian Bach compuso un canon cuya partitura, al ejecutarse, guarda semejanza con la forma de una Banda de Möbius.[1]
El libro de cuentos Queremos tanto a Glenda, del escritor argentino Julio Cortázar, publicado en 1980, cuenta con una composición titulada Anillo de Moebius.[4]
El artista M. C. Escher utilizó la banda de Moebius como motivo principal en diversas obras.[5]
Véase también
Referencias
Referencias no matemáticas
Enlaces externos
Wikimedia Commons alberga contenido multimedia sobre Banda de Möbius. Commons- El rincón de la Ciencia: La banda de Moebius (Möbius)
- Möbius Strip Video
- Banda de Möbius como un paralelepipedo
Categorías:- Matemática recreativa
- Superficies
- Topología
Wikimedia foundation. 2010.
