- Teorema de los números primos
-
En teoría de números el teorema de los números primos es un resultado sobre la distribución asintótica de los números primos.
Contenido
Enunciado del teorema
Sea
 el número de primos que son menores o iguales que
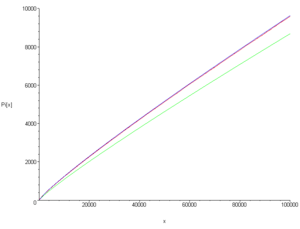
el número de primos que son menores o iguales que  . El teorema establece que:
. El teorema establece que: , donde ln (x) es el logaritmo neperiano de x.
, donde ln (x) es el logaritmo neperiano de x.Esta expresión no implica que la diferencia de las dos partes de la misma para valores de x muy grandes sea cero; sólo implica que el cociente de éstas para valores de
 muy grandes es casi igual a 1.
muy grandes es casi igual a 1.Una mejor aproximación viene dada por el logaritmo integral:
 , donde Li (x) es el logaritmo integral de x.
, donde Li (x) es el logaritmo integral de x.Historia
El teorema de los números primos fue conjeturado por Adrien-Marie Legendre en 1798 y la conjetura fue posteriormente refinada por Gauss con la expresión que actualmente se asocia más frecuentemente al teorema. La demostración formal del teorema la hicieron de forma independiente tanto Jacques Hadamard como Charles-Jean de la Vallée Poussin en el año 1896. Ambas demostraciones se basaban en el resultado de que la función zeta de Riemann
 no tiene ceros de la forma 1 + it con t > 0. En realidad la demostración se hizo sobre una expresión algo más estricta de lo que se indica en la definición anterior del teorema, siendo la expresión demostrada por Hadamard y Poussin la siguiente:
no tiene ceros de la forma 1 + it con t > 0. En realidad la demostración se hizo sobre una expresión algo más estricta de lo que se indica en la definición anterior del teorema, siendo la expresión demostrada por Hadamard y Poussin la siguiente:
donde
 .
.Desde 1896 la expresión asociada al teorema de los números primos ha sido mejorada sucesivamente, siendo la mejor aproximación actual la dada por:

donde
 se define como la función asintótica a
se define como la función asintótica a  y
y  es una constante indeterminada.
es una constante indeterminada.Para valores de
 pequeños se había demostrado que
pequeños se había demostrado que  , lo que llevó a conjeturar a varios matemáticos en la época de Gauss que
, lo que llevó a conjeturar a varios matemáticos en la época de Gauss que  era una cota superior estricta de
era una cota superior estricta de  (esto es que la ecuación
(esto es que la ecuación  no tiene soluciones reales). No obstante, en 1912 J. E. Littlewood demostró que dicha cota es cruzada para valores de
no tiene soluciones reales). No obstante, en 1912 J. E. Littlewood demostró que dicha cota es cruzada para valores de  suficientemente grandes. El primero de ellos se conoce como primer número de Skewes, y actualmente se sabe que es inferior a
suficientemente grandes. El primero de ellos se conoce como primer número de Skewes, y actualmente se sabe que es inferior a  , aunque se piensa que puede ser inferior incluso a
, aunque se piensa que puede ser inferior incluso a  . En 1914 Littlewood amplió su demostración con la inclusión de múltiples soluciones a la ecuación
. En 1914 Littlewood amplió su demostración con la inclusión de múltiples soluciones a la ecuación  . Muchos de estos valores y hallazgos están asociados a la validez de la hipótesis de Riemann.
. Muchos de estos valores y hallazgos están asociados a la validez de la hipótesis de Riemann.Relación con la hipótesis de Riemann
Dada la conexión que hay entre la función zeta de Riemann ζ(s) y π(x), la hipótesis de Riemann es muy importante en teoría de números, y por supuesto, en el teorema de los números primos.
Si la hipótesis de Riemann se cumple, entonces el término error que aparece en el teorema de los números primos puede acotarse de la mejor manera posible. Concretamente, Helge von Koch demostró en 1901 que
si y sólo si la hipótesis de Riemann se cumple. Una variante refinada del resultado de Koch, dada por Lowel Schoenfeld en 1976, afirma que la hipótesis de Riemann es equivalente al siguiente resultado:
Aproximaciones para el enésimo número primo
Como consecuencia del teorema de los números primos, se obtiene una expresión asintótica para el enésimo número primo, denotado por pn:
Una aproximación mejor es:
Referencias
- ↑ Michele Cipolla (1902). «La determinazione assintotica dell'nimo numero primo». Matematiche Napoli 3: pp. 132-166.
- Dorian Goldfeld. «The elementary proof of the prime number theorem:An historical perspective» (en inglés) (PDF). Consultado el 10 de febrero de 2011.
Enlaces externos
- Weisstein, Eric W. «Prime Number Theorem» (en inglés). MathWorld. Wolfram Research.
- Prime number theorem en PlanetMath
Categorías:- Teoría multiplicativa de números
- Teoremas de teoría de números
Wikimedia foundation. 2010.