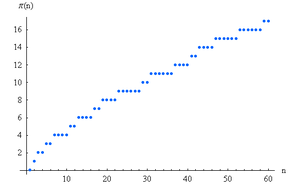
Función contador de números primos

Función contador de números primos
Los 60 primeros valores de π(n).

En matemática, la función contador de números primos es una función que cuenta el número de números primos menores o iguales a cierto número real x. Se denota mediante \scriptstyle\pi(x) (no debe confundirse con el número π) y analíticamente , se define como:

\pi (x) = \# \{p \in \mathbb{P} \mid p \le x\}

donde # significa la cantidad de números que cumplen la condición. Algunos valores son:

π(1) = 0 (no hay primos ≤ 1)
π(2) = 1 (único primo ≤ 2: 2)
π(3) = 2 (primos ≤ 3: 2 y 3)
π(4) = 2 (id.)
π(5) = 3 (primos ≤ 5: 2, 3 y 5)
...
π(10) = 4 (primos ≤ 10: 2, 3, 5 y 7)
...

Teorema de los números primos

Artículo principal: Teorema de los números primos

Una de las consecuencias más importantes de la teoría de números es que el valor de π(x) se aproxima al de x/ln x cuando x tiende al infinito. Es decir:

\pi(x)\sim\frac{x}{\ln x}

Esto no significa que la diferencia entre π(x) y x/ln x se aproxime a cero, sino que su cociente se aproxima a 1. Este resultado, aventurado por primera vez por Carl Friedrich Gauss, se denomina teorema de los números primos. Tras muchos intentos fallidos de demostración, los matemáticos Jacques Hadamard y Charles de la Vallée-Poussin consiguieron, de forma independiente, una demostración definitiva.

Si se expresa la relación anterior cómo

\frac{\pi(x)}{x}\sim\frac{1}{\ln x}

se puede interpretar como que la densidad media de números primos entre los números enteros se aproxima a 1/lnx a medida que x aumenta.

25 años después de que Gauss descubriera la aproximación Legendre lo mejoró aún más:

\pi(x)\sim\frac{x}{\ln x - 1.08366}

Referencias

  • Bach, Eric; Shallit, Jeffrey (1996). «8.8». Algorithmic Number Theory. 1. Ed. MIT Press. p. 234. ISBN 0-262-02405-5. 
  • Weisstein, Eric W.. «Prime Counting Function» (en inglés). MathWorld. Consultado el 28 de abril de 2009.

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Función zeta de Riemann — ζ(s) en el plano complejo. El color de un punto s codifica el valor de ζ(s): Colores fuertes denotan valores cercanos a 0 y el tono codifica el valor del argumento. El punto blanco en s=1 es el polo de la función zeta; los puntos negros en el eje …   Wikipedia Español

  • Hipótesis de Riemann — Parte real (rojo) y parte imaginaria (azul) de la línea crítica Re(s) = 1/2 de la función zeta de Riemann. Pueden verse los primeros ceros no triviales en Im(s) = ±14,135, ±21,022 y ±25,011 …   Wikipedia Español

  • Constante de Legendre — La constante de Legendre (B o B L) es una constante matemática que se presenta en una fórmula propuesta por Adrien Marie Legendre que, según conjeturaba, explicaba el comportamiento asintótico de la función contador de números primos . Se sabe… …   Wikipedia Español

  • Algoritmo — Los diagramas de flujo sirven para representar algoritmos de manera gráfica. En matemáticas, ciencias de la computación y disciplinas relacionadas, un algoritmo (del griego y latín, dixit algorithmus y éste a su vez del matemático persa Al… …   Wikipedia Español

  • División por tentativa — Saltar a navegación, búsqueda La división por tentativa es el algoritmo de factorización de enteros más sencillo y fácil de entender. Dado un entero compuesto n (a lo largo de este artículo, n será el entero a factorizar ), la división por… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”