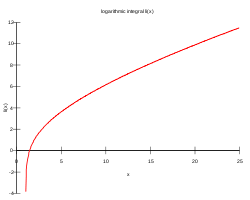
Logaritmo integral

Logaritmo integral
Integral logarítmica representada para valores x>2.

En matemática, la función integral de logaritmo o integral logarítimica li(x), es una funcion especial de relevancia significativa en problemas de física y teoría de números, ya que da una estimación de la cantidad de números primos menores que un determinado valor (teorema de los números primos).

Se define como:

{\rm li} (x) = \int_{0}^{x} \frac{dt}{\ln (t)} \,

Contenido

Representación de la integral

La integral logarítmica tiene una representacion en forma de integral definida para todos los números reales positivos x\ne 1 mediante la integral

{\rm li} (x) = \int_0^x \frac{dt}{\ln (t)}. \;

Donde, ln denota el logaritmo natural. La función 1 / ln(t) tiene una singularidad en t = 1, y la integral para x > 1 tiene que ser interpretada utilizando el valor principal de Cauchy:

{\rm li} (x) = \lim_{\varepsilon \to 0+} \left( \int_0^{1-\varepsilon} \frac{dt}{\ln (t)} + \int_{1+\varepsilon}^x \frac{dt}{\ln (t)} \right). \;

Integral logarítmica desplazada

La integral logarítmica desplazada o integral logarítmica euleriana es definida como

{\rm Li}(x) = {\rm li}(x) - {\rm li}(2) \,

o

{\rm Li} (x) = \int_2^x \frac{dt}{\ln t} \,

Como tal, esta representación integral tiene la ventaja de que evita la singularidad en el dominio de integración.

Esta función es una buena aproximación del número de primos menores que un número dado x.

Representación en forma de serie

La función li(x) está relacionada con la integral exponencial Ei(x) mediante la ecuación

\hbox{li}(x)=\hbox{Ei}(\ln(x)) , \,\!

que es válida para x > 1. Esta identidad proporciona una representación en forma de serie de li(x) como:

{\rm li} (e^u) = \hbox{Ei}(u) = \gamma + \ln u + \sum_{n=1}^\infty {u^{n}\over n \cdot n!} \quad \text{ para } u \ne 0 \; ,

donde γ ≈ 0.57721 56649 01532 ... es la constante de Euler-Mascheroni. Una serie más rápida en términos de convergencia fue dada por Ramanujan:

{\rm li} (x) = \gamma + \ln \ln x + \sqrt{x} \sum_{n=1}^\infty \frac{ (-1)^{n-1} (\ln x)^n} {n! \, 2^{n-1}} \sum_{k=0}^{\lfloor (n-1)/2 \rfloor} \frac{1}{2k+1} .

Valores especiales

La función li(x) tiene un cero simple positivo que se obtiene para el valor x ≈ 1.45136 92348 ...; este número es más conocido como la constante de Ramanujan-Soldner.

li(2) ≈ 1.045163 780117 492784 844588 889194 613136 522615 578151…

Expansión asintótica

El comportamiento asintótico de la función cuando x → ∞ es

{\rm li} (x) = \mathcal{O} \left( {x\over \ln x} \right) \; .

donde \mathcal{O} significa cota superior asintótica. La expansión asintótica completa es

{\rm li} (x) \sim \frac{x}{\ln x} \sum_{k=0}^\infty \frac{k!}{(\ln x)^k}

o

\frac{{\rm li} (x)}{x/\ln x} \sim 1 + \frac{1}{\ln x} + \frac{2}{(\ln x)^2} + \frac{6}{(\ln x)^3} + \cdots.

Nótese, que como expansión asintótica, esta serie es no convergente. Ésta es una aproximación razonable sólo si la serie se trunca para un número finito de términos, y sólo cuando se emplean valores para x suficientemente grandes. Esta expansión se deduce directamente de la expansión asintótica de la integral exponencial.

Uso en teoría de números

Artículo principal: Teorema de los números primos

La integral logarítmica es importante en teoría de números, ya que es utilizada para hacer una estimación de la cantidad de números primos menores que un valor dado. Por ejemplo, el teorema de los números primos asegura que:

\pi(x)\sim\hbox{li}(x)\sim\hbox{Li}(x) \,\!

donde π(x) denota la cantidad de números primos que hay para un valor menor o igual a x.

Referencias


Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Integral exponencial — Gráfica de la función E1 (arriba) y de la función Ei (parte inferior). En el ámbito de las matemáticas la integral exponencial es una función especial definida en el plano complejo e identificada con el símbolo  Ei. Contenido …   Wikipedia Español

  • Logaritmo natural — Gráfica de Logaritmo natural Definición …   Wikipedia Español

  • Logaritmo complejo — Una única rama del logaritmo complejo. El tono del color se utiliza para mostrar el argumento (ángulo de coordenadas polares) del logaritmo complejo. La intensidad del color se utiliza para mostrar el módulo del logaritmo complejo. La página con… …   Wikipedia Español

  • Logaritmo — (Del gr. logos, razón + arithmos , número.) ► sustantivo masculino 1 MATEMÁTICAS Exponente al que es necesario elevar una cantidad positiva para que resulte un número determinado. FRASEOLOGÍA logaritmo común o decimal MATEMÁTICAS El que tiene por …   Enciclopedia Universal

  • Función polilogarítmica — El polilogaritmo (también conocido como función de Jonquière) es una función especial definida por la siguiente serie: Esta no es, en general, una función elemental, aunque esté relacionada con la función logarítmica. La definición dada arriba es …   Wikipedia Español

  • Teorema de los números primos — En teoría de números el teorema de los números primos es un resultado sobre la distribución asintótica de los números primos. Contenido 1 Enunciado del teorema 2 Historia 3 Relación con la hipótesis de Riemann …   Wikipedia Español

  • Anexo:Funciones matemáticas — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Número primo — Un número primo es un número natural mayor que 1, que tiene únicamente dos divisores distintos: él mismo y el 1. Se contraponen así a los números compuestos, que son aquellos que tienen algún divisor natural aparte de sí mismos y del 1. El número …   Wikipedia Español

  • Fórmula explícita — En matemática, la fórmula explícita para funciones L son un conjunto de ecuaciones que relacionan sumas sobre «ceros complejos» o «no triviales» de una función L con sumas sobre potencias de primos, introducida por primera vez por Bernhard… …   Wikipedia Español

  • Función gamma — en el eje real. Valor absoluto de la función gamma en el plano complejo …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”