Números compuestos

Números compuestos

Números compuestos

Todo número natural no primo, a excepción del 1, se denomina compuesto, es decir, tiene uno o más divisores distintos a 1 y a sí mismo.

Los 20 primeros números compuestos son: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30 y 32.

Una característica de los números compuestos es que pueden escribirse como producto de dos enteros positivos menores que él. Así, el número 20 es compuesto porque puede expresarse como 4 x 5; y también el 87 ya que se expresa como 3 x 29. Sin embargo, no es posible hacer lo mismo con el 17 ó el 23 porque son números primos. Cada número compuesto se puede expresar como multiplicación de dos (o más) números primos específicos, cuyo proceso se conoce como factorización.

El número compuesto más pequeño es el 4 y no hay ninguno que sea mayor que todos los demás; hay infinitos números compuestos.

La forma más sencilla de demostrar que un número n es compuesto, es encontrar un divisor d comprendido entre 1 y n (1 < d < n). Por ejemplo, 219 es compuesto porque tiene a 3 por divisor. Y también 371 porque tiene a 7 por divisor. Sin embargo, este método deja de ser efectivo para números que son producto de primos grandes. Una buena alternativa es utilizar entonces el pequeño teorema de Fermat, o mejor la generalización de este teorema debida al matemático suizo Leonhard Euler

Como los números primos y compuestos están entremezclados unos con otros es lógico preguntarse si existirán secuencias de números compuestos consecutivos de longitud arbitraria. La secuencia 32, 33, 34, 35 y 36 es un ejemplo de longitud 5, y 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125 y 126 un ejemplo de longitud 13. La respuesta es que podemos conseguir una secuencia de números compuestos tan larga como se desee. Si deseamos una secuencia de longitud 20, basta tomar los números 21!+2, 21!+3, 21!+4, ... , 21!+21, ya que el primero es divisible por 2, el segundo por 3, etcétera.

Un teorema de Fermat afirma que si p es primo de la forma 4n+1, entonces puede expresarse de forma única como suma de dos cuadrados. Si un número de la forma 4n+1 puede expresarse como suma de dos cuadrados de dos formas diferentes al menos, entonces el número es compuesto. Euler halló un método de factorización a partir de este hecho. Por ejemplo, si 221 = 112 + 102 = 142 + 52, entonces, 142 - 112 = 102 - 52. Tomando mcd(14+11, 10+5) = mcd(25,15) = 5, y después 25/5 = 5 y 15/5 = 3, y por último 52 + 32 = 25 + 9 = 34, entonces mcd(221, 34) = 17 nos da el factor que buscamos. El 1 y el 0 son casos especiales y no se consideran ni primos ni compuestos.

Véase también

Números
Complejos 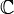\mathbb{C}
Reales \mathbb{R}
Racionales 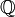\mathbb{Q}
Enteros 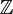\mathbb{Z}
Naturales 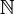\mathbb{N}
Primos
Compuestos
Cero
Negativos
Fraccionarios
Fracción propia
Fracción impropia
Irracionales
Algebraicos
Trascendentes
Imaginarios
Obtenido de "N%C3%BAmeros compuestos"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • números — Existen dos sistemas básicos para representar los números mediante signos: la «numeración arábiga», llamada así porque fue introducida en Occidente por los árabes, y la «numeración romana», heredada de los romanos. Además, los números pueden… …   Diccionario panhispánico de dudas

  • Números pares e impares — En matemática la paridad de un objeto se refiere a si éste es par o impar. En particular, cualquier número entero es par o impar. Un número par es un número entero múltiplo de 2, es decir, un número entero m es número par si y solo si existe otro …   Wikipedia Español

  • Compuestos no estequiométricos — Los compuestos no estequiométricos o bertólidos son un tipo de compuestos químicos en los cuales los elementos que los forman no mantienen proporciones simples y enteras, sino mixtas y variables, en contraposición a los compuestos… …   Wikipedia Español

  • Nomenclatura química de los compuestos inorgánicos — La exactitud de la información en este artículo o sección está discutida. En la página de discusión puedes consultar el debate al respecto …   Wikipedia Español

  • Nomenclatura química de los compuestos orgánicos — La nomenclatura química de los compuestos orgánicos (del griego ονοματοκλήτωρ; όνομα, nombre, y κλήτωρ, llamar. El término latino nomenclatūra se refiere a una lista de nombres, al igual que al nomenclador; esta palabra puede indicar un proveedor …   Wikipedia Español

  • Número primo — Un número primo es un número natural mayor que 1, que tiene únicamente dos divisores distintos: él mismo y el 1. Se contraponen así a los números compuestos, que son aquellos que tienen algún divisor natural aparte de sí mismos y del 1. El número …   Wikipedia Español

  • Número compuesto — Todo número natural no primo, a excepción del 1, se denomina compuesto, es decir, tiene uno o más divisores distintos a 1 y a sí mismo. También se utiliza el término divisible para referirse estos números. Los 20 primeros números compuestos son:… …   Wikipedia Español

  • Criba de Atkin — Saltar a navegación, búsqueda La criba de Atkin es un algoritmo rápido y moderno empleado en matemáticas para hallar todos los números primos menores o iguales que un número natural dado. Es una versión optimizada de la criba de Eratóstenes, pero …   Wikipedia Español

  • Criba de Sundaram — Saltar a navegación, búsqueda La criba de Sundaram es una tabla de los números naturales impares compuestos compuesto por progresiones aritméticas organizadas en las columnas. La criba se basa en el principio de que, al determinar el conjunto de… …   Wikipedia Español

  • Historia de la matemática — Página del Compendio de cálculo por el método de completado y balanceado de Muhammad ibn Mūsā al Khwārizmī (820 d.C.) La historia de las matemáticas es el área de estudio que abarca las investigaciones sobre los orígenes de los descubrimi …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”