Teorema fundamental de homomorfismos

Teorema fundamental de homomorfismos
Commons-emblem-question book orange.svg
 Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas.
Puedes añadirlas así o avisar al autor principal del artículo en su página de discusión pegando: {{subst:Aviso referencias|Teorema fundamental de homomorfismos}} ~~~~

En álgebra abstracta, para un número de estructuras algebraicas, el teorema fundamental de homomorfismos relaciona la estructura de dos objetos entre los cuales se dé un homomorfismo, y del núcleo y de la imagen del homomorfismo.

En la teoría de grupos, el teorema establece lo siguiente:

Si f:G\longrightarrow H es un homomorfismo de grupos y N es un subgrupo normal de G contenido en el núcleo de f, entonces existe un único homomorfismo \bar f tal que \bar f\circ\varphi=f, en donde \varphi:G\longrightarrow G/N es la proyección canónica.

Por otra parte, h es inyectivo y proporciona un isomorfismo entre G/K y la imagen de f.

El homomorfismo \bar f viene dado por

\bar f(g)=f(g)

para todo g de G, y se dice que \bar f es inducido por f\,\!.

El teorema fundamental de homomorfismos también se cumple para los espacios vectoriales, anillos y módulos tomando, respectivamente, ideales y submódulos en lugar de subgrupos normales.

Además

  1. \bar f es un epimorfismo si y sólo si f\,\! lo es.
  2. \ker\bar f=(\ker f/N)
  3. \bar f es un monomorfismo si y sólo si ker f = N


El primer teorema de isomorfía de Noether son consecuencias prácticamente inmediatas de este teorema.


En términos de diagramas conmutativos

El teorema fundamental de homomorfismos puede expresarse también de la siguiente manera: si f:G\longrightarrow H es un homomorfismo de grupos y N es un subgrupo normal de G contenido en el núcleo de f, entonces existe un único homomorfismo \bar f que da lugar al diagrama conmutativo siguiente:

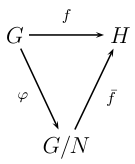
Teo Fund Homo Diag.svg

Véase también

Enlaces externos

Puede verse una demostración de este teorema en el wikilibro de Álgebra, Subgrupos normales.


Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Teorema fundamental sobre homomorfismos — Saltar a navegación, búsqueda En álgebra abstracta, para un número de estructuras algebraicas, el teorema fundamental sobre homomorfismos relaciona la estructura de dos objetos entre los cuales se dé un homomorfismo, y del núcleo y de la imagen… …   Wikipedia Español

  • Teorema fundamental sobre homomorfismos — En álgebra abstracta, para un número de estructuras algebraicas, el teorema fundamental sobre homomorfismos relaciona la estructura de dos objetos entre los cuales se dé un homomorfismo, y del núcleo y de la imagen del homomorfismo. Para los… …   Enciclopedia Universal

  • Teorema fundamental — En matemáticas, hay numerosos teoremas que reciben el nombre de teorema fundamental de distintos campos. Los nombres son generalmente fieles a la tradición, de forma que, por ejemplo, el teorema fundamental de la aritmética se refiere a lo que… …   Wikipedia Español

  • Álgebra de Lie — En matemática, un álgebra de Lie es la estructura algebraica que describe un conjunto de transformaciones infinitesimales. Su uso principal reside en el estudio de objetos geométricos tales como grupos de Lie y variedades diferenciables. El… …   Wikipedia Español

  • Teoremas de isomorfía — Los teoremas de isomorfía, o más propiamente, teoremas de isomorfía de Noether, son tres resultados importantes de la teoría de grupos. Estos teoremas relacionan a los grupos con sus grupos cociente, y son de gran utilidad para construir… …   Wikipedia Español

  • Teoría de grupos — Diagrama de Cayley del grupo libre de orden dos. En álgebra abstracta, la teoría de grupos estudia las estructuras algebraicas conocidas como grupos. Sus objetivos son, entre otros, la clasificación de los grupos, sus propiedades y sus… …   Wikipedia Español

  • Grupo cociente — En teoría de grupos, dado un grupo G y un subgrupo normal N de G, el grupo cociente o grupo factor de G sobre N es, intuitivamente, el grupo que colapsa el grupo normal N al elemento neutro. El grupo cociente se denota por G/N, lo que normalmente …   Wikipedia Español

  • Geometría algebraica — La geometría algebraica es una rama de la matemática que, como sugiere su nombre, combina el álgebra abstracta, especialmente el álgebra conmutativa, con la geometría. Se puede comprender como el estudio de los conjuntos de soluciones de los… …   Wikipedia Español

  • Teoría de haces — En matemática, un haz F sobre un espacio topológico dado, X, proporciona, para cada conjunto abierto U de X, un conjunto F(U), de estructura más rica. A su vez dichas estructuras: F(U), son compatibles con la operación de restricción desde un… …   Wikipedia Español

  • Anillo local — Saltar a navegación, búsqueda En Álgebra abstracta, los anillos locales son ciertos anillos comparativamente simples y que sirven para describir el comportamiento local de las funciones definidas sobre variedades algebraicas o variedades… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”