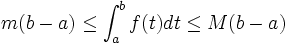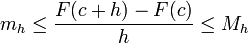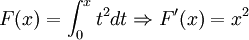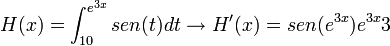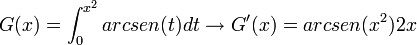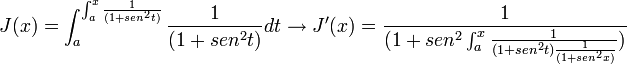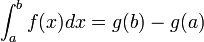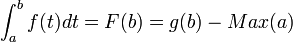- Teorema fundamental del cálculo integral
-
Teorema fundamental del cálculo integral
El teorema fundamental del cálculo integral consiste (intuitivamente) en la afirmación de que la derivación e integración de una función son operaciones inversas. Esto significa que toda función continua integrable verifica que la derivada de su integral es igual a ella misma. Este teorema es central en la rama de las matemáticas denominado análisis matemático o cálculo.
Una consecuencia directa de este teorema es la regla de Barrow, denominada en ocasiones segundo teorema fundamental del cálculo, y que permite calcular la integral de una función utilizando la antiderivada de la función al ser integrada.
Aunque los antiguos matemáticos griegos como Arquímedes ya contaban con métodos aproximados para el cálculo de volúmenes, áreas y longitudes curvas, fue gracias a una idea originalmente desarrollada por el matemático inglés Isaac Barrow y los aportes de Isaac Newton y Gottfried Leibniz que este teorema pudo ser enunciado y demostrado.
Contenido
Intuición geométrica
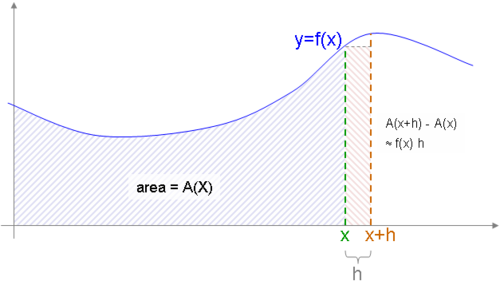
Supóngase que se tiene una función continua y = f(x) y que su representación gráfica es una curva. Entonces, para cada valor de x tiene sentido de manera intuitiva pensar que existe una función A(x) que representa el área bajo la curva entre 0 y x aún sin conocer su expresión.
Supóngase ahora que se quiere calcular el área bajo la curva entre x y x+h. Se podría hacer hallando el área entre 0 y x+h y luego restando el área entre 0 y x. En resumen, el área de esta especie de "loncha" sería A(x+h) − A(x).
Otra manera de estimar esta misma área es multiplicar h por f(x) para hallar el área de un rectángulo que coincide aproximadamente con la "loncha". Nótese que la aproximación al área buscada es más precisa cuanto más pequeño sea el valor de h.
Por lo tanto, se puede decir que A(x+h) − A(x) es aproximadamente igual a f(x) · h, y que la precisión de esta aproximación mejora al disminuir el valor de h. En otras palabras, ƒ(x)·h ≈ A(x+h) − A(x), convirtiéndose esta aproximación en igualdad cuando h tiende a 0 como límite.
Dividiendo los dos lados de la ecuación por h se obtiene
Cuando h tiende a 0, se observa que el miembro derecho de la ecuación es sencillamente la derivada A’(x) de la función A(x) y que el miembro izquierdo se queda en ƒ(x) al ya no estar h presente.
Se muestra entonces de manera informal que ƒ(x) = A’(x), es decir, que la derivada de la función de área A(x) es en realidad la función ƒ(x). Dicho de otra forma, la función de área A(x) es la antiderivada de la función original.
Lo que se ha mostrado es que, intuitivamente, calcular la derivada de una función y "hallar el área" bajo su curva son operaciones "inversas", es decir el objetivo del teorema fundamental del cálculo integral.
Primer teorema fundamental del cálculo
Dada una función f integrable sobre el intervalo [a,b], definimos F sobre [a,b] por
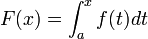 . Si f es continua en
. Si f es continua en 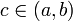 , entonces F es derivable en c y F'(c) = f(c).
, entonces F es derivable en c y F'(c) = f(c).Demostración
Lema
Sea f integrable sobre [a,b] y
Entonces
Demostración
Por definición se tiene que
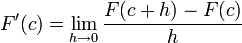 .
.Sea h>0. Entonces
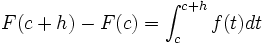 .
.Se define mh y Mh como:
-
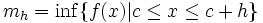 ,
,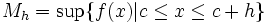
Aplicando el 'lema' se observa que
-
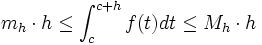 .
.
Por lo tanto,
Sea h < 0. Sean
-
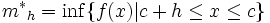 ,
,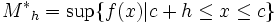 .
.
Aplicando el 'lema' se observa que
-
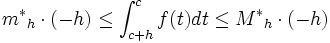 .
.
Como
-
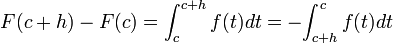 ,
,
entonces
-
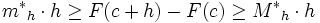 .
.
Puesto que h < 0, se tiene que
-
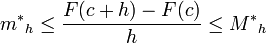 .
.
Y como f es continua en c se tiene que
-
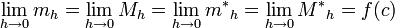 ,
,
y esto lleva a que
-
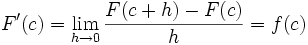 .
.
Ejemplos
Segundo teorema fundamental del cálculo
También se le llama regla de Barrow, en honor a Isaac Barrow o regla de Newton - Leibniz.
Dada una función f continua en el intervalo [a,b] y sea g cualquier función primitiva de f, es decir g'(x)=f(x) para todo
![x \in [a,b]](/pictures/eswiki/56/8290bddba5acf9822dcbf61f4ac67d1b.png) , entonces:
, entonces:Este teorema se usa frecuentemente para evaluar integrales definidas.
Demostración
Sea
-
-
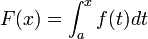 .
.
-
Tenemos por el primer teorema fundamental del cálculo que:
-
-
![F'(x)=f(x)=g'(x) {\ } \forall x \in [a,b]](/pictures/eswiki/52/4b32c18af166be12b79d06455745a669.png) .
.
-
Por lo tanto,
-
-
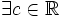 tal que
tal que ![\forall x \in [a,b], F(x)=g(x) + c](/pictures/eswiki/101/ec77e91f6b2579b26889a5ab6135ae1c.png) .
.
-
Observamos que
-
-
- 0 = F(a) = g(a) + c
-
y de eso se sigue que c = − g(a); por lo tanto,
-
-
- F(x) = g(x) − g(a).
-
Y en particular si x = b tenemos que:
Ejemplos
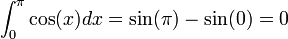
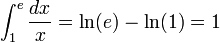
como se puede integrar inmediatamente
Véase también
- Regla de Barrow o Segundo Teorema Fundamental del Cálculo Integral.
- Métodos de integración
- Regla de Leibniz
- Integral de Riemann
Enlaces externos
- El descubrimiento del cálculo integral (Universidad Autónoma de Madrid).
- Interpretación gráfica del Teorema Fundamental del Cálculo (Manuel Sada Allo).
Categorías: Cálculo integral | Teoremas de cálculo
Wikimedia foundation. 2010.

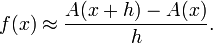
![m \leq f(x) \leq M \forall x \in [a,b]](/pictures/eswiki/48/038b42a32b280aad43eb4056a7e6c3d4.png)