Teoremas de isomorfía

Los teoremas de isomorfía, o más propiamente, teoremas de isomorfía de Noether, son tres resultados importantes de la teoría de grupos. Estos teoremas relacionan a los grupos con sus grupos cociente, y son de gran utilidad para construir isomorfismos entre diversos grupos y grupos cociente.

Pocos cambios no esenciales hacen a estos teoremas válidos también en términos de anillos y módulos en lugar de grupos.

Primer teorema de isomorfía

Sea un homomorfismo de grupos. Entonces existe un isomorfismo , y por tanto

El primer teorema de isomorfía de Noether es una consecuencia inmediata del teorema fundamental de homomorfismos.

Ejemplos

• Considérese el epimorfismo natural dado por

Es claro que si y sólo si , luego , así que

• Si A_n es el subgrupo alternante del grupo simétrico S_n, entonces

Segundo teorema de isomorfía

Si N y H son subgrupos de un grupo G, con N normal en G, entonces

Este segundo teorema de isomorfía se deduce del primero, pues si N es normal a G entonces también lo es , y puede demostrarse que el epimorfismo

cumple con .

Tercer teorema de isomorfía

Si N y H son subgrupos normales de un grupo G, con , entonces

Esto da lugar al diagrama conmutativo siguiente

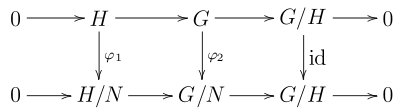
donde φ₁,φ₂ son proyecciones canónicas, es la aplicación identidad y donde las flechas horizontales forman una sucesión de homomorfismos exacta.

Este teorema es también consecuencia del primer teorema de isomorfía. Para una demostración de este teorema, así como de los dos primeros teoremas de ismorfía, véase, por ejemplo, el wikilibro de Álgebra, Subgrupos normales