- Transformada Z
-
En las matemáticas y procesamiento de señales, la Transformada Z convierte una señal real o compleja definida en el dominio del tiempo discreto en una representación en el dominio de la frecuencia compleja.
El nombre de Transformada Z procede de la variable del dominio, al igual que se podría llamar "Transformada S" a la Transformada de Laplace. Un nombre más adecuado para la TZ podría haber sido "Transformada de Laurent", ya que está basada en la serie de Laurent. La TZ es a las señales de tiempo discreto lo mismo que Laplace a las señales de tiempo continuo.
Contenido
Definición
La transformada Z, al igual que otras transformaciones integrales, puede ser definida como una transformada unilateral o bilateral.
Transformada Z bilateral
La TZ bilateral de una señal definida en el dominio del tiempo discreto x[n] es una función X(z) que se define
donde n es un entero y z es, en general, un número complejo de la forma
- z = Aejω
donde A es el módulo de z, y ω es la frecuencia angular en radianes por segundo (rad/s).
Transformada Z unilateral
De forma alternativa, en los casos en que x[n] está definida únicamente para n ≥ 0, la transformada Z unilateral se define como
En el procesamiento de señales, se usa esta definición cuando la señal es causal. En este caso, la Transformada Z resulta una serie de Laurent, con ROC del tipo | z | > R ; es decir que converge "hacia afuera".
Un ejemplo interesante de la TZ unilateral es la función de generación de probabilidades, donde x[n] es la probabilidad que toma una variable discreta aleatoria en el instante n, y la función X(z) suele escribirse como X(s), ya que s = z−1. Las propiedades de las transformadas Z son útiles en la teoría de la probabilidad.
Transformada Z inversa
La Transformada Z inversa se define
donde
 es un círculo cerrado que envuelve el origen y la región de convergencia (ROC). El contorno,
es un círculo cerrado que envuelve el origen y la región de convergencia (ROC). El contorno,  , debe contener todos los polos de
, debe contener todos los polos de  .
.Un caso especial y simple de esta integral circular es que cuando
 es el círculo unidad (que también puede usarse cuando la ROC incluye el círculo unidad), obtenemos la transformada inversa de tiempo discreto de Fourier:
es el círculo unidad (que también puede usarse cuando la ROC incluye el círculo unidad), obtenemos la transformada inversa de tiempo discreto de Fourier:La TZ con un rango finito de n y un número finito de z separadas de forma uniforme puede ser procesada de forma eficiente con el algoritmo de Bluestein. La transformada discreta de Fourier (DFT) es un caso especial de la TZ, y se obtiene limitando z para que coincida con el círculo unidad.
Región de convergencia (ROC)
La región de convergencia, también conocida como ROC, define la región donde la transformada-z existe. La ROC es una región del plano complejo donde la TZ de una señal tiene una suma finita. La ROC para una x[n] es definida como el rango de z para la cual la transformada-z converge. Ya que la transformada–z es una serie de potencia, converge cuando x[n]z − n es absolutamente sumable.
Propiedades de la Region de Convergencia:
La región de convergencia tiene propiedades que dependen de la características de la señal, x[n].
- La ROC no tiene que contener algún polo.Por definición un polo es donde x[z] es infinito. Ya que x[z] tiene que ser finita para todas las z para tener convergencia, no puede existir ningún polo para ROC.
- Si x[n] es una secuencia de duración finita, entonces la ROC es todo el plano-z, excepto en |z|=0 o |z|=∞.
- Si x[n] es una secuencia del lado derecho entonces la ROC se extiende hacia fuera en el ultimo polo desde x[z].
- Si x[n] es una secuencia del lado izquierdo, entonces la ROC se extiende hacia dentro desde el polo mas cercano en x[z].
- Si x[n] es una secuencia con dos lados, la ROC va ser un anillo en el plano-z que esta restringida en su interior y exterior por un polo.
Ejemplo 1 (Sin ROC)
Sea
![x[n] = 0.5^n\](3/ae38b507e5e88ead1c7b0e035cde9046.png) . Expandiendo
. Expandiendo ![x[n]\](4/c1466b9927640af95f78274058d272d9.png) en
en  obtenemos
obtenemosSiendo la suma
No hay ningún valor de
 que satisfaga esta condición.
que satisfaga esta condición.Ejemplo 2 (ROC causal)
Sea
![x[n] = 0.5^n u[n]\](6/57674052f63a5b5b55d69d0b097e5695.png) (donde u es la función escalón). Expandiendo
(donde u es la función escalón). Expandiendo ![x[n]\](4/c1466b9927640af95f78274058d272d9.png) en
en  obtenemos
obtenemosSiendo la suma
La última igualdad se obtiene con la fórmula del sumatorio para series geométricas, y la igualdad sólo se conserva si
 , lo cual puede ser reescrito para definir
, lo cual puede ser reescrito para definir  de modo
de modo  . Por lo tanto, la ROC es
. Por lo tanto, la ROC es  . En este caso la ROC es el plano complejo exterior al círculo de radio 0,5 con origen en el centro.
. En este caso la ROC es el plano complejo exterior al círculo de radio 0,5 con origen en el centro.Ejemplo 3 (ROC anticausal)
Sea
![x[n] = -(0.5)^n u[-n-1]\](0/9508c0a3dd6fab9c51bd316852844bf1.png) (donde u es la función escalón). Expandiendo
(donde u es la función escalón). Expandiendo ![x[n]\](4/c1466b9927640af95f78274058d272d9.png) entre
entre  obtenemos
obtenemosSiendo la suma
De nuevo, usando la fórmula de sumatorio para series geométricas, la iguadad sólo se mantiene si
 , de modo que podemos definir
, de modo que podemos definir  como
como  . Aquí, la ROC es
. Aquí, la ROC es  , es decir, el interior de un círculo centrado en el origen de radio 0,5.
, es decir, el interior de un círculo centrado en el origen de radio 0,5.Conclusión de los ejemplos
Los ejemplos 2 y 3 muestran claramente que la transformada
 de
de ![x[n]\](4/c1466b9927640af95f78274058d272d9.png) es única si y sólo si se especifica cuál es la ROC. Dibujando los gráficos de polos y ceros para los casos causal y anticausal, comprobaríamos como la ROC de ambos casos no incluye el polo que está en 0,5. Esto se extiende a los casos con múltiples polos: la ROC nunca contiene polos.
es única si y sólo si se especifica cuál es la ROC. Dibujando los gráficos de polos y ceros para los casos causal y anticausal, comprobaríamos como la ROC de ambos casos no incluye el polo que está en 0,5. Esto se extiende a los casos con múltiples polos: la ROC nunca contiene polos.En el ejemplo 2, el sistema causal tiene una ROC que incluye
 , mientras que al sistema anticausal del ejemplo 3 le pertenece una ROC que incluye
, mientras que al sistema anticausal del ejemplo 3 le pertenece una ROC que incluye  .
.En los sistemas con múltiples polos, es posible tener una ROC que no incluya ni
 ni
ni  . La ROC crea una región circular. Por ejemplo,
. La ROC crea una región circular. Por ejemplo, ![x[n] = 0.5^nu[n] - 0.75^nu[-n-1]\](b/5bb87341b337d0d121453a4b16d01d31.png) tiene dos polos en 0,5 y 0,75. La ROC será
tiene dos polos en 0,5 y 0,75. La ROC será  , la cual no incluye ni el origen ni el infinito. Este tipo de sistemas se conoce como sistemas de causalidades mezcladas, ya que contiene un término causal
, la cual no incluye ni el origen ni el infinito. Este tipo de sistemas se conoce como sistemas de causalidades mezcladas, ya que contiene un término causal ![0.5^nu[n]\](3/3133def49d00cf59a1e73e28b6988e9c.png) y otro anticausal
y otro anticausal ![-(0.75)^nu[-n-1]\](3/6c39198fd187e5e3a8b2993efc0afceb.png) .
.La estabilidad de un sistema se puede determinar simplemente conociendo su ROC. Si esta ROC contiene el círculo unidad (p. ej.
 ) entonces el sistema es estable. En los sistemas anteriores, el sistema causal es estable porque
) entonces el sistema es estable. En los sistemas anteriores, el sistema causal es estable porque  contiene el círculo unidad.
contiene el círculo unidad.Si tenemos la TZ de un sistema sin su ROC (p.ej., un
![x[n]\](4/c1466b9927640af95f78274058d272d9.png) ambiguo) podemos determinar una única señal
ambiguo) podemos determinar una única señal ![x[n]\](4/c1466b9927640af95f78274058d272d9.png) en función de que queramos o no las siguientes propiedades:
en función de que queramos o no las siguientes propiedades:- Estabilidad
- Causalidad
Si queremos un sistema estable, la ROC debe contener el círculo unidad. Si queremos un sistema causal, la ROC debe contener al infinito. Si queremos un sistema anticausal, la ROC debe contener al origen.
De este modo, podemos encontrar una señal en el tiempo
![x[n]\](4/c1466b9927640af95f78274058d272d9.png) que sea única.
que sea única.Propiedades
- Linealidad. La TZ de una combinación lineal de dos señales en el tiempo es la combinación lineal de sus transformadas en Z.
- Desplazamiento temporal. Un desplazamiento de k hacia la derecha en el dominio del tiempo es una multiplicación por z−k en el dominio de Z.
- Convolución. La TZ de la convolución de dos señales en el tiempo es el producto de ambas en el dominio de Z.
- Diferenciación.
Tabla con los pares más habituales de la transformada Z
Señal, x(n) Transformada Z, X(z) ROC 1 


2 


3 


4 


5 


6 


7 


8 


9 


10 


Relación con Laplace
La TZ bilateral es simplemente la transformada de Laplace bilateral de la señal muestreada
donde
 es la señal continua muestreada,
es la señal continua muestreada, ![x[n]=x(nT) \](7/8178b53ee89bdd11b2bcaedf0b9bef1d.png) la n-ésima muestra,
la n-ésima muestra,  el período de muestreo, y con la sustitución
el período de muestreo, y con la sustitución  .
.Del mismo modo, la TZ unliateral es simplemente la transformada de Laplace unilateral de la señal ideal muestreada. En ambas se asume que la señal muestreada vale cero para todos los índices negativos en el tiempo.
Relación con Fourier
La TZ es una generalización de la transformada de Fourier de tiempo discreto (DTFT). La DTFT puede hallarse evaluando la TZ
 en
en  o, lo que es lo mismo, evaluada en el círculo unidad. Para determinar la respuesta en frecuencia del sistema, la TZ debe ser evaluada en el círculo unidad.
o, lo que es lo mismo, evaluada en el círculo unidad. Para determinar la respuesta en frecuencia del sistema, la TZ debe ser evaluada en el círculo unidad.Ecuación diferencial de coeficientes lineales constantes
La ecuación diferencial de coeficientes lineales constantes (LCCD) es una representación de un sistema lineal basada en la ecuación de la media autorregresiva.
Ambos términos de esta ecuación pueden dividirse por
 , si no es cero, normalizando
, si no es cero, normalizando  la ecuación LCCD puede ser escrita
la ecuación LCCD puede ser escritaEsta forma de la ecuación LCCD es más explícita para comprobar que la salida actual
![y[{n}]\](d/70d386fe8fc517002af609527dc843e1.png) se define en función de las salidas anteriores
se define en función de las salidas anteriores ![y[{n-p}]\](b/b7b5966e8e057221625214b957825fbc.png) , la entrada actual
, la entrada actual ![x[{n}]\](6/f669ef1c4bd8099c03a6b172887ce5eb.png) , y las entradas anteriores
, y las entradas anteriores ![x[{n-q}]\](f/2cf5f29f8bd6fcecfc773b18536e913c.png) .
.Función de transferencia
Se calcula haciendo la TZ de la ecuación
y dividiendo
Ceros y polos
Gracias al teorema fundamental del álgebra sabemos que el numerador tiene M raíces (llamadas ceros) y el denominador tiene N raíces (llamadas polos). Factorizando la función de transferencia
donde
 es el k-ésimo cero y
es el k-ésimo cero y  es el k-ésimo polo. Los ceros y polos son por lo general complejos, y por tanto se pueden dibujar en el plano complejo.
es el k-ésimo polo. Los ceros y polos son por lo general complejos, y por tanto se pueden dibujar en el plano complejo.En definitiva, los ceros son las soluciones de la ecuación obtenida de igualar el numerador a cero, mientras que los polos son las de la ecuación que se obtiene al igualar a cero el denominador.
Se puede factorizar el denominador mediante la descomposición en fracciones simples, las cuales pueden ser transformadas de nuevo al dominio del tiempo. Haciendo esto obtenemos la respuesta al impulso y la ecuación diferencial de coeficientes lineales constantes del sistema.
Salida del sistema
Si por un sistema
 pasa una señal
pasa una señal  entonces la salida será
entonces la salida será  . Haciendo una descomposición en fracciones simples de
. Haciendo una descomposición en fracciones simples de  y la TZ inversa de cada una de ellas puede encontrarse entonces la salida
y la TZ inversa de cada una de ellas puede encontrarse entonces la salida ![y[n]\](c/2bcb339fea06104a3d20c3ccd0c5ef6f.png) .
.Véase también
Categoría:- Transformaciones integrales
Wikimedia foundation. 2010.

![X(z) = Z\{x[n]\} = \sum_{n=-\infty}^{\infty} x[n] z^{-n} \](d/7dd277c71c1256a3437490679567cfba.png)
![X^{+}(z) = Z^{+}\{x[n]\} = \sum_{n=0}^{\infty} x[n] z^{-n} \](a/e2a99fb60f5b075b50d3fb6db7472c9a.png)
![x[n] = Z^{-1} \{(X(z) \}= \frac{1}{2 \pi j} \oint_{C} X(z) z^{n-1} dz \](9/bc90d40023a6286668225396159ae44c.png)
![x[n] = \frac{1}{2 \pi} \int_{-\pi}^{+\pi} X(e^{j \omega}) e^{j \omega n} d \omega \](f/7ef78bc5ff75cd601cd8a04acd98af55.png)
![ROC = \{z : \sum_{n=-\infty}^{\infty}x[n]z^{-n} < \infty\}\](0/460e7ffaa6721b8e053f88c5c2b39885.png)
![x[n] = \{..., 0.5^{-3}, 0.5^{-2}, 0.5^{-1}, 1, 0.5, 0.5^2, 0.5^3, ...\} = \{..., 2^3, 2^2, 2, 1, 0.5, 0.5^2, 0.5^3, ...\}\](7/4b7911745788a91f69782bcbbeb69286.png)
![\sum_{n=-\infty}^{\infty}x[n]z^{-n} < \infty\](c/c7c6c24c9bfbc720a05c008c2b2ab84d.png)
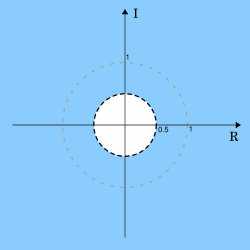
 muestra del círculo.
muestra del círculo.![x[n] = \{..., 0, 0, 0, 1, 0.5, 0.5^2, 0.5^3, ...\}\](8/d48a3129b4a953d236ea7a2b6fcfeea1.png)
![\sum_{n=-\infty}^{\infty}x[n]z^{-n} = \sum_{n=0}^{\infty}0.5^nz^{-n} = \sum_{n=0}^{\infty}\left(\frac{0.5}{z}\right)^n = \frac{1}{1 - 0.5z^{-1}}\](4/fe4a8cc833658dbcab3e63cd6c47cfc3.png)
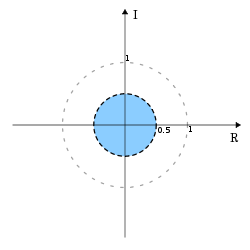
![x[n] = \{..., -(0.5)^{-3}, -(0.5)^{-2}, -(0.5)^{-1}, 0, 0, 0, ...\}\](9/929000b566f8a45560c1b41a005f0ecc.png)
![\sum_{n=-\infty}^{\infty}x[n]z^{-n} = -\sum_{n=-\infty}^{-1}0.5^nz^{-n} = -\sum_{n=-\infty}^{-1}\left(\frac{z}{0.5}\right)^{-n}\](6/1e6a35a12a88d07372c071a528f1b5d1.png)

![Z(a_1 x_1[n] + a_2 x_2[n]) = a_1 Z(x_1[n]) + a_2 Z(x_2[n]) \](f/36f6b889cc0a78a1c90f6dc539f989a7.png)
![Z(x[n-k]) = z^{-k}Z(x[n]) \](7/f07b9e1d20af6113958e4afc1581d6f5.png)
![Z(\{x[n]\} \bigodot \! \! \! \! \! \! \star \ \ \{y[n]\}) = Z(\{x[n]\}) Z(\{y[n]\}) \](6/2f63cb5864ba85771dc7ea59cbbaf93f.png)
![Z(\{nx[n]\}) = \ -z \frac{dZ(\{x[n]\})}{dz} \](9/64951182929de9f383a8f2ab35b6ae8a.png)
![x(t)\sum_{n=-\infty}^{\infty} \delta(t-nT) = \sum_{n=-\infty}^{\infty} x[n] \delta(t-nT) \](1/6e14e7d16619564a3ff140572f86e1a6.png)
![\sum_{p=0}^{N}y[n-p]\alpha_{p} = \sum_{q=0}^{M}x[n-q]\beta_{q}\](5/dc56f77192c3d0d2dafc3bf76362f500.png)
![y[n] = \sum_{q=0}^{M}x[n-q]\beta_{q} - \sum_{p=1}^{N}y[n-p]\alpha_{p}\](7/647e9803e9dbc3ac6e7b4b481b2ef995.png)


