Algoritmo símplex

Un sistema de desigualdades lineales define un politopo como una región factible. El algoritmo simplex comienza en un vértice y se mueve a lo largo de las aristas del politopo hasta que alcanza el vértice de la solución óptima.

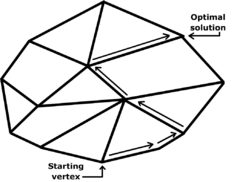
En la teoría de optimización, el algoritmo símplex, descubierto por el matemático norteamericano George Bernard Dantzig en 1947, es una técnica popular para dar soluciones numéricas del problema de la programación lineal. Un método sin relación, pero llamado de manera similar, es el método Nelder-Mead o método símplex cuesta abajo, debido a Nelder y Mead (1965), que es un método numérico para optimización de problemas libres multidimensionales, perteneciente a la clase más general de algoritmos de búsqueda. El que permite encontrar una solución óptima en un problema de maximización o minimización, buscando en los vértices del polígono.

En ambos casos, el método usa el concepto de un símplex, que es un politopo de N + 1 vértices en N dimensiones: un segmento de línea sobre una línea, un triángulo sobre un plano, un tetraedro en un espacio de tres dimensiones y así sucesivamente.

Entrada del problema

Considerar un problema de programación lineal,

maximizar

sujeto a

El algoritmo símplex requiere que el problema de programación lineal esté en la forma aumentada de la programación lineal. El problema puede ser escrito como sigue, en forma de matriz:

Maximizar Z en:

donde x son las variables desde la forma estándar, x_s son las variables de holgura introducidas en el proceso de aumentación, c contiene los coeficientes de optimización, describe el sistema de ecuaciones contraídas, y Z es la variable a ser maximizada.

El sistema es típicamente no determinado, desde que el número de variables excede el número de ecuaciones. La diferencia entre el número de variables y el número de ecuaciones nos da los grados de libertad asociados con el problema. Cualquier solución, óptima o no, incluirá un número de variables de valor arbitrario. El algoritmo símplex usa cero como valor arbitrario, y el número de variables con valor cero es igual a los grados de libertad.

Valores diferentes de cero son llamados variables básicas, y valores de cero son llamadas variables no básicas en el algoritmo símplex.

Esta forma simplifica encontrar la solución factible básica inicial, dado que todas las variables de la forma estándar pueden ser elegidas para ser no básicas (cero), mientras que todas las nuevas variables introducidas en la forma aumentada, son básicas (diferentes de cero), dado que su valor puede ser calculado trivialmente ( para ellas, dado que la matriz problema aumentada en diagonal es su lado derecho)

En cada una de las desigualdades que se plantean en el modelo matemático de programación lineal, se plantean desigualdades de <, >, <=, >=, o =, estas desigualdades se convierten en igualdades completando con variables de holgura si se trata de menor o igual que, o menor que, en el caso de que sea mayor o igual que o mayor que, se completa con variables de excedente, estas con signo negativo ya que como su nombre lo indica, es una cantidad que esta de excedente y hay que quitar para convertirla en igualdad, en caso se maneje el =, se manejan las variables artificiales.

Véase también

• George Dantzig
• Programación lineal
• Conjetura de Hirsch

Enlaces externos

• Ejercicios resueltos utilizando el Método Simplex Módulo de resolución para resolver modelos de Programación Lineal utilizando el Método Simplex
• Ejemplos clásicos resueltos por el Método Simplex.
• Método Simplex Aquí se explica en detalle la teoría del Método Simplex, la lógica subyacente y se dan ejemplos de solución del mismo.
• Ejemplos en JAVA (incluyen código)
• Herramienta para resolver problemas mediante el método Simplex, método de las Dos Fases, y método Gráfico por alumnos de la Universidad de Málaga (UMA, España).
• Complex Aplicación gráfica realizada integramente en java para resolver problemas mediante el método de penalización y el método de las Dos Fases. Muestra paso a paso la matriz de resolución. Recomendado para verificar la correcta resolución de problemas mediante tablas.
• Linear Program Solver (LiPS) está destinado a resolver problemas de programación lineal. Principales características: fácil de usar interfaz gráfica, análisis de sensibilidad, la meta y el solucionador de programación entera mixta. LiPS apoya MPS y el formato LP.