- Cobertura de aristas
-
En teoría de Grafos , una covertura de aristas de un grafo es un conjunto de aristas donde cada vertice del grafo es incidente en al menos en una arista del conjunto. En ciencias de la computación, el problema de la cobertura mínima de arista es el problema de encontrar una covertura de aristas de tamaño minimo. Este es un problema de optimización que pertenece a la clase de problemas de covertura y puede resolverse en tiempo polinomial.
Definición
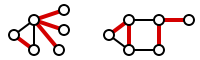
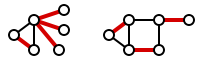
Formalmente, una cobertura de aristas sobre el grafo G es un conjunto de aristas C donde cada vértice es incidente con al menos una arista en C. Se dice que el conjunto C cubre los vértices de G. La siguiente imagen muestra ejemplos de covertura de aristas en dos grafos.
Una cobertura de aristas mínima es una cobertura de aristas del menor tamaño posible. El número de cubrimiento de aristas ρ(G) es el tamaño de una cobertura de aristas mínima. La siguiente imagen muestra ejemplos de la cobertura de aristas mínima.
Notar que en la figura de la derecha no solo es una cobertura de aristas si no también un matching. En particular, es un matching perfecto: un maching M en donde cada vértice es incidente con exactamente una arista en M. Un matching perfecto es siempre una cobertura de aristas mínima.
Véase también
Referencias
- Weisstein, Eric W. «Edge Cover» (en inglés). MathWorld. Wolfram Research.
- Garey, Michael R.; Johnson, David S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, ISBN 0-7167-1045-5.
Wikimedia foundation. 2010.