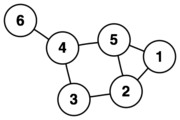
A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal correspondiente. Todos los ejemplos están basados en la imagen de la derecha.

A B C D E F G H I J K L M N Ñ O P Q R S T U V W X Y Z

A

Adyacencia

Véase Vecindad.

Árbol

Un árbol es un grafo conexo simple acíclico. Algunas veces, un vértice del árbol es distinguido llamándolo raíz. Los árboles se usan frecuentemente como estructuras de datos en ciencias de la computación (véase árbol).

Arco

Véase Arista.

Arista

Una arista o arco es una relación matemática que conecta dos vértices. Una arista dirigida es una arista de un digrafo y tiene una dirección asociada consigo, esto es, posee un vértice inicial y un vértice final. Una arista no dirigida es una donde no se distingue un vértice inicial ni uno final.

B

Bosque

Un bosque es un conjunto de árboles; o de forma equivalente, un bosque es un grafo acíclico.

Bucle

Un bucle o loop en un grafo o digrafo es una arista que conecta al mismo vértice consigo mismo.

Búsqueda en profundidad

La Búsqueda en profundidad o DFS (Depth First Search) es un algoritmo que permite recorrer todos los vértices de un grafo de manera ordenada, pero no uniforme.

C

Camino

Un camino es una sucesión de vértices tal que de cada uno de sus vértices existe una arista hacia el vértice sucesor. Un camino simple es aquel en que todas las aristas del camino son diferentes.

Dos caminos son ajenos o independientes si no tienen ningún vértice en común excepto el primero y el último.

La longitud de un camino es el número de aristas que usa dicho camino, contando aristas recorridas varias veces el mismo número de veces que las recorramos. En el ejemplo, (1, 2, 5, 1, 2, 3) es un camino con longitud 5, y (5, 2, 1) es un camino simple de longitud 2.

Camino euleriano

Un camino euleriano en un grafo es un camino que usa cada arista una y sólo una vez. Si existe tal camino decimos que el grafo es atravesable. Esta definición es dual a la de camino hamiltoniano.

Camino hamiltoniano

Existe un concepto dual al de camino/ciclo Euleriano. Un camino Hamiltoniano en un grafo es un camino que "visita" cada vértice una y sólo una vez; y un ciclo Hamiltoniano es un ciclo que visita cada vértice una y sólo una vez.

El ejemplo de la imagen posee un camino hamiltoniano.

Ciclo

Un Ciclo (o circuito) es un camino que empieza y acaba en el mismo vértice. Los ciclos de longitud 1 son los bucles. En el ejemplo, (1, 2, 3, 4, 5, 2, 1) es un ciclo de longitud 6.

Un ciclo simple es un ciclo que tiene como longitud al menos 3 y en el que el vértice del comienzo sólo aparece una vez más y como vértice final, y los demás sólo aparecen una vez. En el grafo de arriba (1, 5, 2, 1) es un ciclo simple.

Ciclo euleriano

Un ciclo euleriano en un grafo es un ciclo que usa cada arista una y sólo una vez.

Ciclo hamiltoniano

Un ciclo hamiltoniano en un grafo es un ciclo que visita cada vértice una y sólo una vez.

Clique

Una clique en un grafo es un conjunto de vértices tal que para todo par de vértices, existe una arista que las conecta. En el ejemplo, los vértices 1, 2 y 5 forman una clique de tamaño 3.

Cobertura de vértices

La cobertura de vértices, covering o recubrimiento de vértices de un grafo es un conjunto de vértices cuyos elementos son adyacentes a todos los demás vértices del grafo.

Coloreo de grafos

El coloreo de grafos o coloración de grafos es quizá el problema NP-completo más afamado de la teoría de grafos, y consiste en asignarle distintos colores o marcas a los vértices de un grafo, de manera que ningún par de vértices adyacentes compartan el mismo color o marca.

Componente fuertemente conexo

Un componente fuertemente conexo es un grafo tal que para cada par de vértices, existe un camino de uno hacia el otro, y viceversa. Los componentes fuertemente conexos de un grafo dirigido son sus subgrafos máximos fuertemente conexos. Estos subgrafos forman una partición del grafo.

Conjunto estable

Véase Conjunto independiente.

Conjunto independiente

Un conjunto independiente en un grafo es un conjunto de vértices tal que ninguno es adyacente a otro. En el ejemplo, los vértices 1,3, y 6 forman un conjunto tal y los 3,5, y 6 forman otro conjunto independiente.

Covering

Véase Cobertura de vértices.

D

Depth First Search

Véase Búsqueda en profundidad.

DFS

Véase Búsqueda en profundidad.

Digrafo

Es un grafo cuyas aristas son dirigidas, es decir, cada arista posee un vértice inicial y uno final.

G

Girth

El girth de un grafo es la longitud del ciclo simple más corto en el grafo. El "girth" de un grafo acíclico se define como infinito.

Grado

El grado o valencia de un vértice es el número de aristas incidentes en él. Para un grafo con bucles, éstos son contados por dos. En el ejemplo, los vértices 1 y 3 tienen grado 2; los vértices 2, 4 y 5, grado 3; y el vértice 6, grado 1.

En un dígrafo, podemos distinguir el grado saliente (el número de aristas que dejan el vértice) y el grado entrante (el número de aristas que entran en un vértice). El grado de un vértice sería la suma de ambos números.

Grafo

Un grafo es un conjunto de vértice o nodos unidos por aristas o arcos.

Grafo acíclico

Un grafo se dice acíclico si no contiene ningún ciclo simple.

Grafo bipartido

Un grafo bipartido es cualquier grafo cuyos vértices pueden ser divididos en dos conjuntos, tal que no haya aristas entre los vértices del mismo conjunto. Se ve que un grafo es bipartido si no hay ciclos de longitud impar. Ver grafo completo bipartido

Un grafo k-partido o grafo k-colorable es un grafo con cuyos vértices se puede hacer una partición en k subconjuntos disjuntos tal que no haya aristas entre vértices del mismo subconjunto. Un grafo 2-partido es lo mismo que un grafo bipartido.

Un grafo k-partido se dice semiregular si cada partición tiene un grado uniforme.

Grafo completo

Un grafo completo es un grafo simple en el que cada vértice es adyacente a cualquier todo otro vértice. El del ejemplo no es completo. El grafo completo en n vértices se denota a menudo por K_n. Tiene n(n-1)/2 aristas (correspondiendo a todas las posibles elecciones de pares de vértices).

Grafo conexo

Si es posible formar un camino desde cualquier vértice a cualquier otro en el grafo, decimos que el grafo es conexo. Si es posible hacer esto incluso tras quitar k-1 vértices, decimos que el grafo es k-conexo.

Un grafo es k-conexo si y sólo si contiene k caminos independientes entre cualesquiera dos vértices. Teorema de Menger El grafo ejemplo es conexo (y por tanto 1-conexo), pero no es 2-conexo.

Grafo dirigido

Véase Digrafo.

Grafo nulo

El grafo nulo es el grafo cuyos conjuntos de aristas y de vértices son vacíos.

Grafo plano

Un grafo plano es uno que puede ser dibujado en el plano sin que se intersecten cualesquiera dos aristas. El del ejemplo lo es; el grafo completo en n vértices, para n> 4, no es plano.

Grafo ponderado

Un grafo ponderado asocia un valor o peso a cada arista en el grafo. El peso de un camino en un grafo con pesos es la suma de los pesos de todas las aristas atravesadas.

Grafo regular

Un grafo regular es un grafo cuyos vértices tienen todos el mismo grado.

Grafo simple

Un grafo simple es un grafo o digrafo que no tiene bucles, y que no es un multigrafo.

Grafo universal

Un grafo universal en una clase K de grafos es un grafo en el que puede incluirse como subgrafo todo elemento de K.

Grafo vacío

Un grafo vacío es el grafo cuyo conjunto de aristas es vacío.

I

Incidencia

Véase Vecindad.

L

Loop

Véase Bucle.

M

Matriz de adyacencia

Una matriz de adyacencia es una matriz de n x n que permite representar un grafo o digrafo finito, donde cada valor en la posición (i,j) representa el número de aristas desde el vértice i-ésimo al j-ésimo.

N

Nodo

Véase Vértice.

P

Puente

Un puente a es una arista tal que si la quitamos nos quedamos con un grafo con una componente conexa más que el original.

Punto de articulación

Un punto de articulación o punto de corte es un vértice tal que si lo quitamos nos quedamos con un grafo con más componentes conexas que el original.

Punto de corte

Véase Punto de articulación.

R

Recubrimiento de vértices

Véase Cobertura de vértices.

S

Subárbol

Un subárbol de un grafo G es un subgrafo que es además un árbol.

Subgrafo

Un subgrafo de un grafo G es un grafo cuyo conjunto de vértices es un subconjunto del de G, cuyo conjunto de aristas es un subconjunto del conjunto de las aristas de G, y tal que la aplicación w es la restricción de la aplicación de G.

Subgrafo de expansión

Un subgrafo de expansión de un grafo G es un subgrafo con el mismo conjunto de vértices que G. Un árbol expansión es un subgrafo expansión que es un árbol. Cada grafo tiene un árbol de expansión.

T

Teoría espectral

La teoría espectral es aquella que estudia las relaciones entre las propiedades de la matriz de adyacencia y las de su grafo.

Torneo

Un torneo es un grafo dirigido completo, simple, no generalizado, no degenerado y sin dígonos.

V

Valencia

Véase Grado.

Vértice

Un vértice o nodo es la unidad fundamental de la que están formados los grafos.

Vecindad

Dos vértices son vecinos, adyacentes o incidentes si existe una arista entre ellos. En el ejemplo, el vértice 1 tiene dos vecinos: el vértice 2 y el 5. Para un grafo simple, el número de vecinos de un vértice es igual a su grado.