Función Xi de Riemann

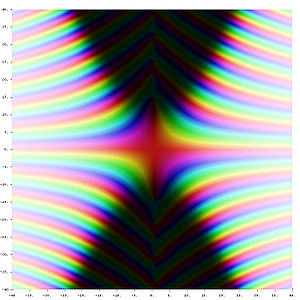Función xi de Riemann

ξ(s)

en el plano complejo. El color de un punto

s

codifica el valor de la función. Colores fuertes denotan valores cercanos a cero y el tono codifica el valor del argumento.

En matemática, la la función Xi de Riemann es una variante de la función zeta de Riemann, y es definida así por la particularidad de tener una ecuación funcional simple. La función se llama así en honor a Bernhard Riemann.

Definición

La función xi (minúscula) de Riemann es definida como:

$\xi(s) = \frac{1}{2} s(s-1) \pi^{-\frac{s}{2}} \Gamma\left(\frac{s}{2}\right) \zeta(s).$

La ecuación funcional (o fórmula de reflexión) para esta la función xi es

$\xi(1-s)=\xi(s).\,$

The función Xi (mayúscula) está definica como

$\Xi(s) = \pi^{-\frac{s}{2}} \Gamma\left(\frac{s}{2}\right) \zeta(s)$

y también obedece a la misma ecuación funcional.

Valores

La fórmula general para enteros pares es

$\xi(2n) = (-1)^{n+1}{{B_{2n}2^{2n-1}\pi^{n}(2n^2-n)(n-1)!} \over {(2n)!}}.$

Por ejemplo:

$\xi(2) = {\pi \over 6}.$

Representación en forma de serie

La función xi tiene la siguiente expansión en forma de serie:

$\frac{d}{dz} \ln \xi \left(\frac{-z}{1-z}\right) = \sum_{n=0}^\infty \lambda_{n+1} z^n.$

Esta expansión juega particularmente un papel importante en el criterio de Li, en el cual declara que la hipótesis de Riemann es equivalente a tener $λ n > 0$ para todo número positivo n.

Hipótesis de Riemann

Como se ha señalado por varios trabajos de Alain Connes y otros, la hipótesis de Riemann ies equivalente a la afirmación de que la función xi de Riemann es el determinante funcional del operador

$-D^{2}+f(x) \,$

con

$f^{-1}(x) = \sqrt (4\pi) \frac{d^{1/2}N(x)}{dx^{1/2}}$ así,

$\frac{\xi(1/2+iz)}{\xi(1/2)}= \frac{\det(H-z^{2})}{\det(H)}$ ,

cuya conjetura está apoyada mediante varias evaluaciones numéricas.

Referencias

Weisstein, Eric W. «Xi-Function» (en inglés). MathWorld. Wolfram Research.
«Power series expansions of Riemann's xi function». Mathematics of Computation 58 (198): pp. 765–773. 1992. doi:10.1090/S0025-5718-1992-1122072-5. Bibcode: 1992MaCom..58..765K.
Riemann Ξ function en PlanetMath

Categoría:

Funciones Zeta y L

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

Función zeta de Riemann — ζ(s) en el plano complejo. El color de un punto s codifica el valor de ζ(s): Colores fuertes denotan valores cercanos a 0 y el tono codifica el valor del argumento. El punto blanco en s=1 es el polo de la función zeta; los puntos negros en el eje … Wikipedia Español
Función zeta de Riemann — En matemáticas, la función zeta de Riemann zeta es una función de gran importancia en teoría de números, debido a su relación con la distribución de los números primos … Enciclopedia Universal
Producto de Euler para la función zeta de Riemann — Saltar a navegación, búsqueda En 1737 Leonhard Euler probó un resultado que abrió las puertas de la moderna teoría de números ( teoría analítica de números ) enunciando el siguiente teorema: Si s > 1, entonces … Wikipedia Español
Función divisor — σ0(n) representada hasta n=250. Función divis … Wikipedia Español
Función eta de Dirichlet — η(s) en el plano complejo. El color en un punto s codifica el valor de η(s). Colores fuertes denotan valores cercanos a cero y el tono codifica el valor del argumento. En las matemáticas, en el área … Wikipedia Español
Función gamma — en el eje real. Valor absoluto de la función gamma en el plano complejo … Wikipedia Español
Función Z — En matemática, la función Z es una función usada para el estudio de la función zeta de Riemann a lo largo de la recta crítica, donde la parte real del argumento es 1/2. Es también llamada función Z de Riemann Siegel o función zeta de Hardy.[1]… … Wikipedia Español
Función meromorfa — En análisis complejo, una función meromorfa sobre un subconjunto abierto D del plano complejo es una función que es holomorfa en todo D excepto en un conjunto de puntos aislados, llamados polos de la función. (La terminología viene del Griego… … Wikipedia Español
Función theta — En matemática, las funciones theta o θ funciones son funciones especiales de varias variables complejas. Son importantes en diversas áreas, incluidas las teorías de variedades abelianas y espacios móduli, y de las formas cuadráticas. También se… … Wikipedia Español
Función polilogarítmica — El polilogaritmo (también conocido como función de Jonquière) es una función especial definida por la siguiente serie: Esta no es, en general, una función elemental, aunque esté relacionada con la función logarítmica. La definición dada arriba es … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Función Xi de Riemann

Contenido

Definición

Valores

Representación en forma de serie

Hipótesis de Riemann

Referencias

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Función Xi de Riemann

Contenido

Definición

Valores

Representación en forma de serie

Hipótesis de Riemann

Referencias

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo