Función gamma

Función Gamma en el eje real.

Valor absoluto de la función gamma en el plano complejo.

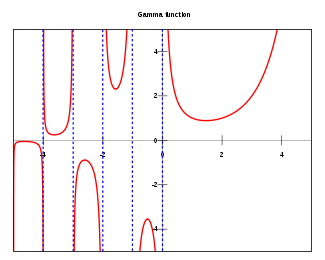
En matemáticas, la función Gamma (denotada como $\scriptstyle \Gamma(z)\,\!$ ) es una función que extiende el concepto de factorial a los números complejos. La notación fue ideada por Adrien-Marie Legendre. Si la parte real del número complejo z es positivo, entonces la integral

$\Gamma(z) = \int_0^\infty t^{z-1} e^{-t}\,dt$

converge absolutamente, esta integral puede ser extendida a todo el plano complejo excepto a los enteros negativos y al cero.

Si n es un entero positivo, entonces

$\Gamma(n) = (n-1)!\,$

lo que nos muestra la relación de esta función con el factorial. De hecho, la función Gamma generaliza el factorial para cualquier valor complejo de n.

La función Gamma aparece en varias funciones de distribución de probabilidad, por lo que es bastante usada tanto en probabilidad y estadística como en combinatoria.

Contenido

1 Definición tradicional
2 Definiciones alternativas
3 Obtención de la ecuación funcional usando integración por partes
4 Propiedades
5 Función Pi
6 Relación con otras funciones
7 Valores de la función Gamma
8 Aproximaciones
9 Aplicaciones de la función gamma
- 9.1 Cálculo fraccionario
10 Véase también
11 Referencias
12 Enlaces externos
- 12.1 Sitios web
- 12.2 Lecturas adicionales

Definición tradicional

La función gamma en el plano complejo.

Si la parte real del número complejo z es positiva (Re(z) > 0), entonces la integral

$\Gamma(z) = \int_0^\infty t^{z-1} e^{-t}\,dt \,\!$

converge absolutamente. Usando la integración por partes, se obtiene la siguiente propiedad:

$\Gamma(z+1)=z \, \Gamma(z)$

Esta ecuación funcional generaliza la relación $n! = n (n - 1)!$ del factorial. Se puede evaluar $Γ(1)$ analíticamente:

$\Gamma(1) = \int_0^\infty e^{-t} dt = \lim_{k \rightarrow \infty} \left. -e^{-t} \right |_0^k = -0 - (-1) = 1.$

Combinando estas dos relaciones se obtiene que el factorial es un caso especial de la función Gamma:

$\Gamma(n+1) = n \, \Gamma(n) = \cdots = n! \, \Gamma(1) = n!\,$

para los números naturales n.

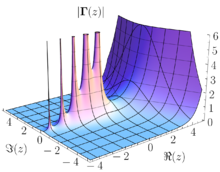
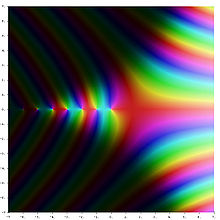
La función Gamma es una función meromorfa de $z\in\mathbb{C}$ con polos simples en $z = -n\,\,(n = 0,\,1,\,2,\,3,\,\dots)$ y residuos $\operatorname{Res}(\Gamma(z),-n) = \frac{(-1)^{n}}{n!}$ .^[1] Estas propiedades pueden ser usadas para extender $Γ(z)$ desde su definición inicial a todo el plano complejo (exceptuando los puntos en los cuales es singular) por continuación analítica.

Definiciones alternativas

Las siguientes definiciones de la función Gamma mediante productos infinitos, debidas a Euler y Weierstrass respectivamente, son válidas para todo complejo z que no sea un entero negativo:

$\begin{align} \Gamma(z) &= \lim_{n \rightarrow \infty } n! \; n^z\prod^{n}_{k=0}\frac{1}{z+k} = \lim_{n \to \infty} \frac{n! \; n^z}{z \, (z+1)\cdots(z+n)} = \frac{1}{z} \prod_{n=1}^\infty \frac{\left(1+\frac{1}{n}\right)^z}{1+\frac{z}{n}} \\ \Gamma(z) &= \frac{e^{-\gamma z}}{z} \prod_{n=1}^\infty \left(1 + \frac{z}{n}\right)^{-1} e^{z/n} \\ \end{align}$

donde $γ$ es la constante de Euler-Mascheroni.

Es sencillo mostrar que la definición de Euler satisface la ecuación funcional dada arriba como sigue. Dado $z\neq 0,\,-1,\,-2,\,-3,\,\dots$

$\begin{align} \Gamma(z+1) &= \lim_{n \to \infty} \frac{n! \; n^{z+1}}{(z+1) \; (z+2)\cdots(z+1+n)} \\ &= \lim_{n \to \infty} \left( z \; \frac{n! \; n^z}{z \; (z+1) \; (z+2)\cdots(z+n)} \; \frac{n}{(z+1+n)}\right) \\ &= z \; \Gamma(z) \; \lim_{n \to \infty} \frac{n}{(z+1+n)} \\ &= z \; \Gamma(z). \\ \end{align}$

También puede obtenerle la siguiente representación integral:

$\Gamma(z+1) = \int_0^\infty e^{-t^{1/z}}\,dt. \,\!$

Obtención de la ecuación funcional usando integración por partes

Obtener $Γ(1)$ es sencillo:

$\Gamma(1) = \int_0^\infty e^{-x} x ^{1-1} dx = \int_0^\infty e^{-x} dx = -e^{-\infty} - (-e^0) = 0 - (-1) = 1$

Ahora obtendremos una expresión para $Γ(n + 1)$ como una función de $Γ(n)$ :

$\Gamma(n + 1) = \int_0^\infty e^{-x} x ^{n + 1 - 1} dx = \int_0^\infty e^{-x} x ^n dx$

Usamos integración por partes para resolver la integral

$\int_0^\infty e^{-x} x ^n dx = \left[\frac{-x^n}{e^x}\right]_0^\infty + n \int_0^\infty e^{-x} x ^{n - 1} dx$

En el límite inferior se obtiene diréctamente $\frac{-0^n}{e^0} = \frac{0}{1} = 0$ .

En el infinito, usando la regla de L'Hôpital:

$\lim_{x \rightarrow \infty} \frac{-x^n}{e^x} = \lim_{x \rightarrow \infty} \frac{-n! \cdot 0}{e^x} = 0$ .

Por lo que se anula el primer término, $\left[\frac{-x^n}{e^x}\right]_0^\infty$ , lo que nos da el siguiente resultado:

$\Gamma(n + 1) = n \int_0^\infty e^{-x} x ^{n - 1} dx$

La parte derecha de la ecuación es exactamente $n Γ(n)$ , con lo que hemos obtenido una relación de recurrencia:

Γ(n + 1) = n Γ(n)

Apliquemos la fórmula a unos pocos valores:

$\Gamma(2) = \Gamma(1 + 1) = 1\Gamma(1) = 1! = 1\,$

$\Gamma(3) = \Gamma(2 + 1) = 2\Gamma(2) = 2 \cdot 1! = 2! = 2\,$

$\Gamma(4) = \Gamma(3 + 1) = 3\Gamma(3) = 3 \cdot 2! = 3! = 6\,$

$\Gamma(n + 1) = n\Gamma(n) = n\cdot(n-1)! = n!$

Propiedades

De la representación integral se obtiene:

$\lim_{z\to 0^+}\Gamma(z)=\lim_{z\to 0^+}\frac{\Gamma(z+1)}{z}=\infty$ .

Otras ecuaciones funcionales importantes de la función Gamma son la fórmula de reflexión de Euler

$\Gamma(1-z) \; \Gamma(z) = {\pi \over \sin{(\pi z)}} \,\!$

y la fórmula de duplicación

$\Gamma(z) \; \Gamma\left(z + \frac{1}{2}\right) = 2^{1-2z} \; \sqrt{\pi} \; \Gamma(2z). \,\!$

La fórmula de duplicación es un caso especial del teorema de multiplicación

$\Gamma(z) \; \Gamma\left(z + \frac{1}{m}\right) \; \Gamma\left(z + \frac{2}{m}\right) \cdots \Gamma\left(z + \frac{m-1}{m}\right) = (2 \pi)^{(m-1)/2} \; m^{1/2 - mz} \; \Gamma(mz). \,\!$

Una propiedad básica y muy útil de la función Gamma , que puede obtenerse a partir de la definición mediante productos infinitos de Euler es:

$\overline{\Gamma(z)} = \Gamma(\overline{z}) \,\!$

Quizá el valor más conocido de la función Gamma con argumento no negativo es

$\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}, \,\!$

La cual puede obtenerse haciendo $z = 1 / 2$ en la fórmula de reflexión o en la fórmula de duplicación, usando la relación de la función Gamma con la función beta dada más abajo con $x = y = 1 / 2$ o haciendo la sustitución $u = \sqrt{t}$ en la definición integral de la función Gamma, con lo que se obtiene una integral Gaussiana. En general, para valores impares de n se tiene:

$\Gamma\left(\frac{n}{2}+1\right)= \sqrt{\pi}\, \frac{n!!}{2^{(n+1)/2}}$ (n impar)

donde n!! denota al doble factorial.

Las derivadas de la función Gamma vienen dadas por la función poligamma. Por ejemplo:

$\Gamma'(z)=\Gamma(z)\psi_0(z). \,\!$

A partir de la representación integral de la función Gamma, se obtiene que su derivada n-ésima es:

${d^{n} \over (dx)^{n}}\,\Gamma(x) = \int_0^\infty t^{x-1} e^{-t} \ln^{n} t\,dt.$

La función Gamma tiene un polo de orden 1 en $z = - n$ para todo número natural y el cero. El residuo en cada polo es:

$\operatorname{Res}(\Gamma,-n)=\frac{(-1)^n}{n!}. \,\!$

El teorema de Bohr-Mollerup dice que, entre todas las funciones que generalizan el factorial de los números naturales a los reales, sólo la función Gamma es logaritmo convexa (o log-convexa), esto es, el logaritmo natural de la función Gamma es una función convexa.

El desarrollo en Serie de Laurent de $Γ(z)$ para valores 0 < z < 1 es:

$\Gamma(z) \approx \frac{1}{z} -\gamma + \left[\frac{\gamma^2}{2!}+ \frac{\zeta(2)}{2} \right]z+ \left[\frac{\gamma^3}{3!}+ \frac{\zeta(2)}{2}\gamma+ \frac{\zeta(3)}{3} \right]z^2+ \dots$

Donde $ζ(n)$ es la función zeta de Riemann.

Función Pi

Gauss introdujo una notación alternativa de la función Gamma denominada función Pi, que en términos de la función Gamma es:

$\Pi(z) = \Gamma(z+1) = z \; \Gamma(z), \,\!$

Así, la relación de esta función Pi con el factorial es bastante más natural que en el caso de la función Gamma:

$\Pi(n) = n!.\!$

La fórmula de la reflexión toma la siguiente forma:

$\Pi(z) \; \Pi(-z) = \frac{\pi z}{\sin( \pi z)} = \frac{1}{\operatorname{sinc}(z)} \,\!$

Donde sinc es la función sinc normalizada, el teorema de la multiplicación se escribe así:

$\Pi\left(\frac{z}{m}\right) \, \Pi\left(\frac{z-1}{m}\right) \cdots \Pi\left(\frac{z-m+1}{m}\right) = \left(\frac{(2 \pi)^m}{2 \pi m}\right)^{1/2} \, m^{-z} \, \Pi(z). \,\!$

A veces se encuentra la siguiente definición

$\pi(z) = \frac{1}{\Pi(z)}, \,\!$

donde $π(z)$ es una función entera, definida para todo número complejo, pues no tiene polos. La razón de ello es que la función Gamma y, por tanto, la función Pi, no tienen ceros.

Relación con otras funciones

En la representación integral de la función Gamma, tanto el límite superior como el inferior de la integración están fijados. La función gamma incompleta superior $γ(a, x)$ e inferior $Γ(a, x)$ se obtienen modificando los límites de integración superior o inferior respectivamente.

$\Gamma(a,x) = \int_x^{\infty} t^{a-1}\,e^{-t}\,dt .\,\!$

$\gamma(a,x) = \int_0^x t^{a-1}\,e^{-t}\,dt .\,\!$

La función Gamma está relacionada con la función beta por la siguiente fórmula

$\Beta(x,y)=\frac{\Gamma(x) \; \Gamma(y)}{\Gamma(x+y)}. \,\!$

La derivada logarítmica de la función Gamma es la función digamma $ψ (0) (z)$ . Las derivadas de mayor orden son las funciones poligamma $ψ (n) (z)$ .

$\psi(x) =\psi^0(x) = \frac{\Gamma'(x)}{\Gamma(x)}$

$\psi^{(n)}(x) = \left(\frac{d}{dx}\right)^n \psi(x) = \left(\frac{d}{dx}\right)^{n+1} \log\Gamma(x)$

El análogo de la función Gamma sobre un cuerpo finito o un anillo finito son las sumas gaussianas, un tipo de suma exponencial.
La función gamma inversa es la inversa de la función gamma, que es una función entera.
La función Gamma aparece en la definición integral de la función zeta de Riemann $ζ(z)$ :

$\zeta(z) = \frac{1}{\Gamma(z)}\int_{0}^{\infty} \frac{u^{z-1}}{e^u - 1} \; \mathrm{d}u \,\!.$

Fórmula válida sólo si $\operatorname{Re}(z) > 1$ . También aparece en la ecuación funcional de $ζ(z)$ :

$\pi^{-z/2} \; \Gamma\left(\frac{z}{2}\right) \zeta(z) = \pi^{-\frac{1-z}{2}} \; \Gamma\left(\frac{1-z}{2}\right) \; \zeta(1-z).$

Valores de la función Gamma

Artículo principal: Valores de la función Gamma

$\begin{array}{lll} \Gamma(-3/2) &= \frac {4\sqrt{\pi}} {3} &\approx 2,363 \\ \Gamma(-1/2) &= -2\sqrt{\pi} &\approx -3,545 \\ \Gamma(1/2) &= \sqrt{\pi} &\approx 1,772 \\ \Gamma(1) &= 0! &= 1 \\ \Gamma(3/2) &= \frac {\sqrt{\pi}} {2} &\approx 0,886 \\ \Gamma(2) &= 1! &= 1 \\ \Gamma(5/2) &= \frac {3 \sqrt{\pi}} {4} &\approx 1,329 \\ \Gamma(3) &= 2! &= 2 \\ \Gamma(7/2) &= \frac {15\sqrt{\pi}} {8} &\approx 3,323 \\ \Gamma(4) &= 3! &= 6 \\ \end{array}$

Aproximaciones

La función Gamma se puede calcular numéricamente con precisión arbitrariamente pequeña usando la fórmula de Stirling o la aproximación de Lanczos.

Para argumentos que sean múltiplos enteros de 1/24, la función Gamma puede ser evaluada rápidamente usando iteraciones de medias aritmético geométricas (véase Valores de la función Gamma).

Debido a que tanto la función Gamma como el factorial crecen muy rápidamente para argumentos moderadamente grandes, muchos programas de computación incluyen funciones que devuelven el logaritmo de la función Gamma. Este crece más lentamente, y en cálculos combinatorios es muy útil, pues se pasa de multiplicar y dividir grandes valores a sumar o restar sus logaritmos.

Aplicaciones de la función gamma

Cálculo fraccionario

Artículo principal: Cálculo fraccional

La n-ésima derivada de $a x b$ (donde n es un número natural) se puede ver de la siguiente manera:

$\frac{d^{n}}{dx^{n}}\left(ax^{b}\right)=\left(b-n+1\right)\cdots\left(b-2\right)\left(b-1\right)bax^{b-n}=\frac{b!}{\left(b-n\right)!}ax^{b-n}$

como $n! = Γ(n + 1)$ entonces $\frac{d^{n}}{dx^{n}}\left(ax^{b}\right)=\frac{\Gamma\left(b+1\right)}{\Gamma\left(b-n+1\right)}ax^{b-n}$ donde n puede ser cualquier número donde gamma esté definido o se pueda definir mediante límites.

De esta manera se puede calcular por ejemplo, la 1/2 derivada de $x$ , de $x 2$ e inclusive de una constante $c = c x 0$ :

$\frac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}\left(x\right)=\frac{2\sqrt{x}}{\sqrt{\pi}}$

$\frac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}\left(x^{2}\right)=\frac{8\sqrt{x^{3}}}{3\sqrt{\pi}}$

$\frac{d^{\frac{1}{2}}}{dx^{\frac{1}{2}}}\left(c\right)=\frac{c}{\sqrt{\pi}\sqrt{x}}$

Véase también

Referencias

↑ George Allen, and Unwin, Ltd., The Universal Encyclopedia of Mathematics. United States of America, New American Library, Simon and Schuster, Inc., 1964. (Forward by James R. Newman)

Philip J. Davis, "Leonhard Euler's Integral: A Historical Profile of the Gamma Function," Am. Math. Monthly 66, 849-869 (1959)
Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function. En formatos PostScript y HTML.
Bruno Haible & Thomas Papanikolaou. Fast multiprecision evaluation of series of rational numbers. Technical Report No. TI-7/97, Darmstadt University of Technology, 1997
Julian Havil, Gamma, Exploring Euler's Constant", ISBN 0-691-09983-9 (c) 2003
Emil Artin, "The Gamma function", in Rosen, Michael (ed.) Exposition by Emil Artin: a selection; History of Mathematics 30. Providence, RI: American Mathematical Society (2006).

Enlaces externos

Wikimedia Commons alberga contenido multimedia sobre Función gamma. Commons

Sitios web

Ejemplos de problemas que involucran a la Función Gamma en Exampleproblems.com (en inglés).
Cephes - Librería de funciones especiales matemáticas de C y C++ (en inglés).
Fast Factorial Functions - Varios algoritmos.
Approximation Formulas - Aproximaciones.
Evaluador de la función Gamma de Wolfram con precisión arbitraria.
Volume of n-Spheres and the Gamma Function en MathPages (en inglés).
Herramienta online para obtener gráficas de funciones que contiene a la función Gamma.

Lecturas adicionales

Milton Abramowitz and Irene A. Stegun, eds. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover, 1972. (See Chapter 6)
G. Arfken and H. Weber. Mathematical Methods for Physicists. Harcourt/Academic Press, 2000. (See Chapter 10.)
Harry Hochstadt. The Functions of Mathematical Physics. New York: Dover, 1986 (See Chapter 3.)
W.H. Press, B.P. Flannery, S.A. Teukolsky, and W.T. Vetterling. Numerical Recipes in C. Cambridge, UK: Cambridge University Press, 1988. (See Section 6.1.)

Categoría:

Funciones gamma y relacionadas

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

Función gamma — En matemáticas, la función gamma es una función que extiende el concepto de factorial a los números complejos. La notación fue ideada por Adrien Marie Legendre. Si la parte real del número complejo z es positivo, entonces la integral converge… … Enciclopedia Universal
Función gamma incompleta — En matemática, la función gamma se define como una integral definida. La función gamma incompleta se define como una integral definida del mismo integrando. Hay dos tipos de función gamma incompleta, una para el caso en el que varía el límite… … Wikipedia Español
Función gamma inversa — Gráfica de 1/Γ(x) a lo largo del eje real. Función gamma invers … Wikipedia Español
Función gamma elíptica — En matemática, la función gamma elíptica es una generalización de la función q gamma, la cual es en si misma un q análogo de la función gamma ordinaria. Está íntimamente relacionada con la función estudiada por Jackson (1905), y puede ser… … Wikipedia Español
Función zeta de Riemann — ζ(s) en el plano complejo. El color de un punto s codifica el valor de ζ(s): Colores fuertes denotan valores cercanos a 0 y el tono codifica el valor del argumento. El punto blanco en s=1 es el polo de la función zeta; los puntos negros en el eje … Wikipedia Español
Función digamma — Ψ(s) en el plano complejo. El color de un punto s codifica el valor de Ψ(s).Colores fuertes denotan valores cercanos a cero y el tono codifica el valor del argumento. En matemáticas, la función digamma se define como la … Wikipedia Español
Función polilogarítmica — El polilogaritmo (también conocido como función de Jonquière) es una función especial definida por la siguiente serie: Esta no es, en general, una función elemental, aunque esté relacionada con la función logarítmica. La definición dada arriba es … Wikipedia Español
Función beta — Este artículo trata sobre función beta de Euler. Para otras funciones beta, véase Función beta (desambiguación). Función beta. Representación de la función para valores reales positivos de x e y. En matemáticas, la función beta … Wikipedia Español
Función de Bessel — En matemática, las funciones de Bessel, primero definidas por el matemático Daniel Bernoulli y más tarde generalizadas por Friedrich Bessel, son soluciones canónicas y(x) de la ecuación diferencial de Bessel: (1) donde α es un … Wikipedia Español
Función error — Gráfica de la función error. En matemáticas, la función error (también conocida como función error de Gauss) es una función especial (no elemental) que se utiliza en el campo de la probabilidad, la estadística y las ecuaciones diferenciales… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico