P (clase de complejidad)

Se ha sugerido que este artículo o sección sea fusionado con Tiempo polinómico (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí.

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar al autor principal del artículo en su página de discusión pegando: {{subst:Aviso referencias|P (clase de complejidad)}} ~~~~

Introducción

Los recursos comúnmente estudiados en complejidad computacional son:

– El tiempo: mediante una aproximación al número de pasos de ejecución que un algoritmo emplea para resolver un problema.

– El espacio: mediante una aproximación a la cantidad de memoria utilizada para resolver el problema.

Los problemas se clasifican en conjuntos o clases de complejidad (L, NL, P, PCompleto,NP, NP-Completo, NP Duro...).Nosotros nos vamos a centrar en la clase P.

En el análisis computacional, se requiere un modelo de la computadora para la que desea estudiar el requerimiento en términos de tiempo. Normalmente, dichos modelos suponen que la computadora es determinista (dado el estado actual de la computadora y las variables de entrada, existe una única acción posible que la computadora puede tomar) y secuencial (realiza las acciones una después de la otra). Estas suposiciones son adecuadas para representar el comportamiento de todas las computadoras existentes, aún incluye a las máquinas con computación en paralelo.

En esta teoría, la clase P consiste de todos aquellos problemas de decisión que pueden ser resueltos en una máquina determinista secuencial en un período de tiempo polinomial en proporción a los datos de entrada.En la teoría de complejidad computacional, la clase P es una de las más importantes; la clase NP consiste de todos aquellos problemas de decisión cuyas soluciones positivas/afirmativas pueden ser verificadas en tiempo polinómico a partir de ser alimentadas con la información apropiada, o en forma equivalente, cuya solución puede ser hallada en tiempo polinómico en una máquina no-determinista.

La principal pregunta, aún sin respuesta, en la teoría de la computación está referida a la relación entre estas dos clases: ¿P=NP?

La clase P

P suele ser la clase de problemas computacionales que son “eficientemente resolubles” o “tratables”, aunque haya clases potencialmente más grandes que también se consideran tratables, como RP Y BPP. Aunque también existen problemas en P que no son tratables en términos prácticos; por ejemplo, unos requieren al menos n^1000000 operaciones.

P es conocido por contener muchos problemas naturales, incluyendo las versiones de decisión de programa lineal, cálculo del máximo común divisor, y encontrar una correspondencia máxima.

Problemas notables en P

Algunos problemas naturales son completos para P, incluyendo la conectividad (o la accesibilidad) en grafos no dirigidos.

Una generalización de P es NP, que es la clase de lenguajes decidibles en tiempo polinómico sobre una máquina de Turing no determinista. De forma trivial, tenemos que P es un subconjunto de NP. Aunque no está demostrado, la mayor parte de los expertos creen que esto es un subconjunto estricto.

Aquí, EXPTIME es la clase de problemas resolubles en tiempo exponencial. De todas las clases mostradas arriba, sólo se conocen dos contenciones estrictas:

• • P estrictamente está contenido en EXPTIME.
  • L estrictamente está contenida en PSPACE.

Los problemas más difíciles en P son los problemas P-completos

Otra generalización de P es el Tiempo polinómico No uniforme (P/Poly)[1]. Si un problema está en P/poly, entonces puede solucionarse en un tiempo polinomial determinado el cual, dado una cadena, este solo depende de la longitud de la entrada. A diferencia de NP, no se comprueban las cadenas defectuosas que entran en la máquina de Turing, puesto que no es un verificador.

P/poly es una clase grande que contiene casi todos los algoritmos prácticos, incluyendo todo el BPP. Si esta contiene a NP, la jerarquía polinomial se colapsa con el segundo nivel. Por otra parte, esta también contiene algunos algoritmos poco prácticos, incluyendo algunos problemas no decidibles.

Propiedades

Los algoritmos de tiempo polinómico son cerrados respecto a la composición. Intuitivamente, esto quiere decir que si uno escribe una función con un determinado tiempo polinómico y consideramos que las llamadas a esa misma función son constantes y, de tiempo polinómico, entonces el algoritmo completo es de tiempo polinómico. Esto es uno de los motivos principales por los que P se considera una máquina independiente; algunos rasgos de esta máquina, como el acceso aleatorio, es que puede calcular en tiempo polinómico el tiempo polinómico del algoritmo principal reduciéndolo a una máquina más básica.

Las pruebas existenciales de algoritmos de tiempo polinómico

Se conoce que algunos problemas son resolubles en tiempo polinómico, pero no se conoce ningún algoritmo concreto para solucionarlos. Por ejemplo, el teorema Robertson-Seymour garantiza que hay una lista finita de los menores permitidos que compone (por ejemplo) el conjunto de los grafos que pueden ser integrados sobre un toroide; además, Robertson y Seymour demostraron que hay una complejidad O (n3) en el algoritmo para determinar si un grafo tiene un grafo incluido. Esto nos da una prueba no constructiva de que hay un algoritmo de tiempo polinómico para determinar si dado un grafo puede ser integrado sobre un toroide, a pesar de no conocerse ningún algoritmo concreto para este problema.

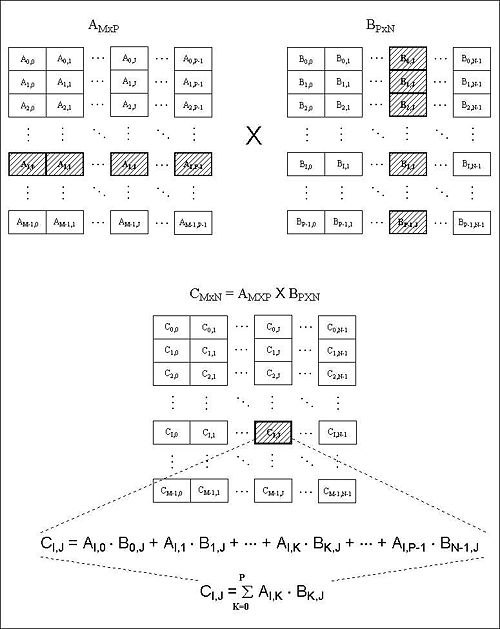
Ejemplo: Multiplicación matricial

Dadas dos matrices A y B de tamaño n x n, hallar C, el producto de las dos. Un primer algoritmo se saca de la definición de producto de matrices: Ci,j es el producto escalar de la i-ésima fila por la j-ésima columna. Su tiempo de ejecución sería O(n³):

int i,j,k;
int A[n][n],B[n][n],C[n][n];
 
// Dar valores a A y B.
 
for(i=0;i<n;i++)
  {
  for(j=0;j<n;j++) 
    {
     for(k=0;k<n;k++)
       C[i][j]+=A[i][k]*B[k][j];
    }
 }

Pero este tiempo de ejecución también se puede mejorar. Si n es una potencia de 2, se pueden dividir A, B y C en cuatro submatrices cada una, de la forma:

Ahora, para hallar las submatrices de C, basta con utilizar que:

C(1,1) = A(1,1)·B(1,1) + A(1,2)·B(2,1)

C(1,2) = A(1,1)·B(1,2) + A(1,2)·B(2,2)

C(2,1) = A(2,1)·B(1,1) + A(2,2)·B(2,1)

C(2,2) = A(2,1)·B(1,2) + A(2,2)·B(2,2)

Con este método el tiempo de ejecución es de T(n) = 8·T(n/2) + O(n²), o lo que es lo mismo, O(n³), con lo que no habría diferencia entre este método y el primero propuesto. Hay que reducir el número de multiplicaciones por debajo de 8. Esto se logra utilizando el algoritmo de Strassen. Definimos las siguientes matrices:

M1 = (A1,2 - A2,2)·(B2,1 + B2,2)

M2 = (A1,1 + A2,2)·(B1,1 + B2,2)

M3 = (A1,1 - A2,1)·(B1,1 + B2,1)

M4 = (A1,1 + A1,2)·B2,2

M5 = A1,1·(B1,2 - B2,2)

M6 = A2,2·(B2,1 - B1,1)

M7 = (A2,1 + A2,2)·B1,1

para las que se necesitan 7 multiplicaciones diferentes, y ahora se calculan las submatrices de C utilizando sólo sumas:

C1,1 = M1 + M2 - M4 + M6 C1,2 = M4 + M5 C2,1 = M6 + M7 C2,2 = M2 - M3 + M5 - M7

El nuevo tiempo de ejecución es de T(n) = 7·T(n/2) + O(n²), es decir, de T(n) = O(nlog27) = O(n2.81). Este algoritmo sólo es mejor que el directo cuando n es muy grande, y es más inestable cuando se utiliza con números reales, por lo que tiene una aplicabilidad limitada.

Para el caso general en el que n no es potencia de 2, se pueden rellenar las matrices con ceros hasta que las dos matrices sean cuadradas y n sea una potencia de 2.

Otros ejemplos

Camino Mínimo: Encontrar el camino mínimo desde un vértice origen al resto de los vértices.

Ciclo Euleriano: Encontrar un ciclo que pase por cada arco de un grafo una única vez.

Quicksort: Forma de ordenación rápida