Ciclo euleriano

Un ciclo euleriano es aquel camino que recorre todas las aristas de un grafo pasando una y sólo una vez por cada arco (arista) del grafo, siendo condición necesaria que regrese al vértice inicial de salida (ciclo = camino en un grafo donde coinciden vértice inicial o de salida y vértice final o meta). Una definición más formal lo define como: "aquel ciclo que contiene todas las aristas de un grafo solamente una vez".

En relación con los ciclos eulerianos Carl Hierholzer publicó la primera caracterización completa de los grafos eulerianos en 1873, probando matemáticamente que de hecho los grafos eulerianos son exactamente aquellos grafos que están conectados con todos y donde cada uno de los vértices tienen grado par.

Ciclos eulerianos

ejemplo.

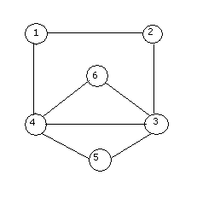
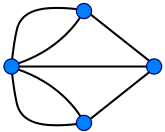
En la imagen, es un ciclo euleriano, luego es un grafo euleriano.

Un grafo es una representación, un modelo, compuesto por un número determinado de vértices (nodos) y un número de arcos (aristas) que los relacionan, cada arista o arco tiene la capacidad de relacionar dos nodos. La palabra ciclo se emplea en teoría de grafos para indicar un camino cerrado en un grafo, es decir, en que el nodo de inicio y el nodo final son el mismo, como contrapartida un camino hamiltoniano es un camino que recorre todos los vértices de un grafo sin pasar dos veces por el mismo vértice. Si el camino es cerrado se dice un ciclo hamiltoniano.

Si un grafo admite un ciclo euleriano, se denomina grafo euleriano.

Historia

El origen de la teoría de los ciclos eulerianos fue planteado y resuelto por el propio Leonhard Euler en 1736 en un problema que tiene el nombre de Siete puentes de la ciudad de Königsberg (Prusia oriental en el siglo XVIII y actualmente, Kaliningrado, provincia rusa) dando origen a la Teoría de los grafos.

El problema se enuncia de la siguiente forma: Dos islas en el río Pregel, en Königsberg se unen entre ellas y con la tierra firme mediante siete puentes. ¿Es posible dar un paseo empezando por una cualquiera de las cuatro partes de tierra firme, cruzando cada puente una sola vez y volviendo al punto de partida?

Euler enfocó el problema representando cada parte de tierra por un punto y cada puente, por una línea, uniendo los puntos que se corresponden. Entonces, el problema anterior se puede trasladar a la siguiente pregunta: ¿se puede recorrer el dibujo sin repetir las líneas?

Euler demostró que no era posible puesto que el número de líneas que inciden en cada punto no es par (condición necesaria para entrar y salir de cada punto, y para regresar al punto de partida, por caminos distintos en todo momento).

Teorema

Dado no orientado y conexo (no existen nodos aislados) valen las siguientes expresiones.

1) es euleriano;

2) con grado y par.

3) todos disjuntos en los arcos, es decir con

Propiedades

• Un grafo conexo y no dirigido se dice que es euleriano si cada vértice tiene un grado par.
• Un grafo no dirigido es euleriano si es conexo y si se puede descomponer en uno con los vértices disjuntos.
• Si un grafo no dirigido G es euleriano entonces su gráfo-línea L(G) se dice que es también euleriano.
• Un grafo dirigido es euleriano si es conexo y cada vértice tiene grados internos iguales a los externos.
• Un grafo no dirigido se dice que es susceptible de ser recorrido (en inglés: traversable) si es conexo y al menos dos vértices en el grafo tienen grado impar.

Contando circuitos eulerianos en digrafos

El número de circuitos euleriano en los digrafos puede ser calculado mediante el teorema denominado en Inglés: BEST-theorem, procedente de los nombres de sus fundadores: dígrafo euleriano G := (V, E), el número ciclos eulerianos no-equivalentes en el grafo es

o equivalentemente

siendo C cualquier cofactor de la matriz laplaciana de G.

Véase también

• Problema de los puentes de Königsberg
• Ciclo hamiltoniano
• Glosario en teoría de grafos
• Camino euleriano

Referencias

• "Solutio problematis ad geometriam situs pertinentis", Euler, L.,Comment. Academiae Sci. I. Petropolitanae 8 (1736), 128-140.
• "Über die Möglichkeit, einen Linienzug ohne Wiederholung und ohne Unterbrechnung zu umfahren",Hierholzer, C. Mathematische Annalen 6 (1873), 30-32.
• Récréations Mathématiques IV, Lucas, E., Paris, 1921.
• "Deux problemes de geometrie de situation", Fleury, Journal de mathematiques elementaires (1883), 257-261.