Suma de Minkowski

En geometría, la suma de Minkowski es una operación sobre las partes de un espacio vectorial. A dos partes A y B asocia su conjunto suma, formado por la suma de los elementos de A y B:

La suma de dos compactos es compacta, así es posible restringir la operación a este conjunto, que puede ser provisto con una distancia llamada distancia de Hausdorff. La suma de Minkowski es entonces una operación continua. Además, respeta la convexidad, es decir, que la suma de dos convexos es convexa. La medida de la suma de dos convexos verifica una mayoración, denominada la desigualdad de Brunn-Minkowski.

La suma de Minkowski interviene en muchas áreas de las matemáticas puras y aplicadas. Esta herramienta es la base de muchas demostraciones de teoremas isoperimétricos para determinar la parte del espacio de mayor volumen posible dada como restricción la magnitud de su frontera. En la geometría euclidiana, se tienen las esferas de dimensión n. La suma de Minkowski también está involucrada al contar el número de caras de un poliedro, resolver preguntas de mosaicos o aún para estudiar la geometría de los convexos. Se aplican, por ejemplo, en cristalografía por razones de teselaciones del espacio, en economía para optimizar el potencial de producción de un grupo de empresas, o aún para estudiar las mezclas.

Preámbulo

Ejemplos

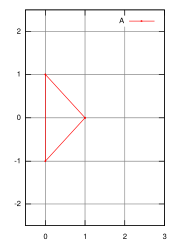
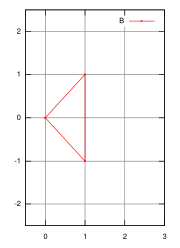
El conjunto A de la izquierda es un triángulo cuyas coordenadas de sus vértices son (0, -1), (0,1) y (1.0). A la derecha se muestra un triángulo B similar, orientado de manera diferente. Las coordenadas son (0,0), (1, -1) y (1.1). Si los conjuntos A y B son dos tripletas, se tiene:

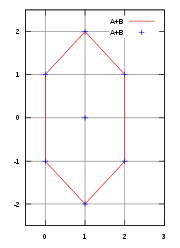
Si A y B son los triángulos rojos, se forma un hexágono, ilustrado en la parte inferior derecha.

En general, la suma de dos polígonos es todavía un polígono. Esta propiedad es verdadera para un poliedro de cualquier dimensión.

Uno puede notar la analogía entre la suma de Minkowski y la convolución. Figurativamente, se puede obtener la superficie de la suma de dos conjuntos A + B cubriendo B de pintura y haciendo recorrer a su centro la superficie A. Por esta razón, la suma de Minkowski es a veces llamada convolución de A y B.

Evidentemente, la suma de un conjunto A y un singleton {b} corresponde a la traslación de A por el vector b.

La suma de Minkowski de conjuntos. La suma de de los cuadrados Q₁=[0, 1]² y Q₂=[1, 2]² es el cuadrado Q₁+Q₂=[1, 3]².

Es algo más complejo darse cuenta de que la suma de dos cuadrados es de nuevo un cuadrado. En general, si C es un conjunto convexo, simétrico con respecto al origen, la suma C + C es igual al convexo 2C, aquí 2C significa la homotecia de razón 2. La prueba es algo más sutil, es análoga al lema preliminar usado en la prueba del teorema de Minkowski. Para realizar esto, se puede observar que cada elemento de 2C es un elemento de C + C, recíprocamente sea u + v un elemento de C + C, se escribe también como el doble de 1/2(u + v), o este elemento es en C.

Podemos citar un último ejemplo, que se encuentra en théorème isopérimétrique (Wikipedia en francés). Sean C un compacto convexo de un plano euclidiano y P un polígono convexo cuyos vértices están todos en la frontera de C y cuya arista más grande es de una longitud limitada (mayorada) por ε. Entonces, la suma de P y del disco con centro el vector nulo y radio ε contiene el compacto convexo C. Esta propiedad es un paso para establecer que no hay superficie más grande que el disco de mismo perímetro.

Véase también

• Convolución
• Teorema de Minkowski
• En morfología matemática la suma de Minkowski sirve para definir la dilatación

Enlaces externos

• M. Rousset Sommes de Minkowski de triangles Thèse de troisième cycle, Université Joseph Fourier 1996

Referencias

• Dacorogna, Bernard (2004). Imperial College Press. ed (en inglés). Introduction to the Calculus of Variations. Londres. ISBN 1-86094-508-2.