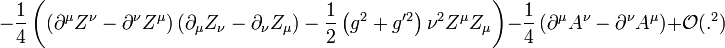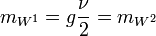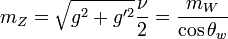- Bosones W y Z
-
Bosones W y Z
Bosones W± y Z0 Clasificación Partícula elemental Familia Bosón Grupo Bosón de gauge Interacción Gravedad
ElectromagnetismoSímbolo(s) W± y Z0 Antipartícula W+: Bosón W−
Z0: Ella mismaMasa W±: 80,401 (38) GeV/c2
Z0: 91,1876 (21) GeV/c2Vida media ~10−25 s Carga eléctrica W±: ±1 e
Z0: NeutraCarga de color Neutra Espín 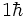
Los bosones W y Z son las partículas mediadoras de la interacción nuclear débil, una de las cuatro interacciones fundamentales de la naturaleza. Son tres tipos de partículas fundamentales muy masivas que se encargan en general de cambiar el sabor de otras partículas, los leptones y los quarks.
Fueron descubiertas en el CERN, en 1983; aunque su existencia y características generales habían sido predichas mucho antes. El bosón W recibe ése nombre de la palabra inglesa 'weak', por la interacción débil a la que caracteriza. El bosón Z puede haber recibido ése nombre por ser el último de los tres en descubrirse, o tal vez por tener carga eléctrica 'zero'. En español también se suelen conocer como 'bosones intermedios'.
Contenido
Propiedades
Existen dos tipos de bosones W: uno con carga eléctrica positiva igual a la carga elemental y el otro con la misma carga pero negativa. Se simbolizan W+ y W− y ambos son respectivamente antipartículas del otro. El bosón Z es eléctricamente neutro, y es su propia antipartícula.
Los tres tipos de bosones son muy masivos para ser partículas elementales Los bosones W tienen una masa de 80.4 GeV/c2,[1] y el bosón Z de 91.2 GeV/c2. Son más masivos que los núcleos de hierro, lo que explica perfectamente que las distancias a las que ésta interacción actúa sean tan pequeñas, del orden de 10-18 m.
Los tres bosones tienen un spin de 1, y una vida media muy corta del orden de 10-25 segundos.
W y Z en la interacción débil
Cuando un leptón o un quark parece convertirse en uno más ligero (se desintegra o decae), se dice que cambian de sabor. Todos los procesos de cambio de sabor se deben a la interacción débil, y en todas ellas interviene uno de los tres tipos de bosones intermedios.
Uno de los procesos más importantes en los que intervienen los bosones W es la desintegración beta, en la que un neutrón se 'convierte' en un protón:
Como podemos observar, el neutrón se convierte en un protón y emite además un electrón y un electrón-antineutrino. Pero el neutrón no es una partícula elemental, está hecho de 2 quarks abajo y un quark arriba (y además de gluones), y se convierte en protón porque uno de los quarks abajo cambia su sabor a arriba.
Pero el quark abajo no es el que emite el electrón y el neutrino. De hecho, el quark abajo solo se convierte en el quark arriba y en un bosón W negativo (para conservar la carga eléctrica del sistema). Es el bosón W el que casi instantáneamente después decae en los dos leptones.
En el caso de la emisión de positrones, el bosón intermedio implicado es el positivo; se trata de la conversión de un protón en neutrón, positrón y electrón-neutrino.
Viendo los casos anteriores, el bosón Z debería intervenir en los procesos que no implican cambio en la carga eléctrica de la partícula afectada (pero sí cambio de sabor), pero no es el caso. Éste bosón solo actúa como portador de momento lineal: cuando dos partículas se intercambian un bosón Z una le está pasando momento a la otra. Éste intercambio se llama interacción de corriente neutra, ninguna de las partículas afectadas cambia de sabor y su estudio requiere el uso de los aceleradores de partículas más energéticos del mundo.
Bosones W y Z virtuales
Siguiendo con el ejemplo anterior, vemos que el quark abajo se convierte en un quark arriba y en un bosón W. Esto viola claramente la ley de conservación de la masa-energía, ya que parece imposible que haya tanta energía en el sistema como para que un ligerísimo quark genere de pronto un bosón W que tiene más de 20.000 veces su masa original. Pero el bosón W existe sólo durante unos 10-25 segundos; debido al principio de indeterminación de Heisenberg, existe durante un tiempo tan breve, que no se podrá nunca medir su cantidad de movimiento (función de la masa) y posición con total exactitud.
Sólo hay que tener en cuenta que la masa-energía al final y al principio son equivalentes, y que en medio hubo una asimetría de masa-energía tan breve que es como si la realidad ni se diera cuenta de ella. Las partículas que hacen ése tipo de cosas se llaman partículas virtuales, y se dan también en las otras fuerzas fundamentales, pero la masa de los bosones W y Z hace que ésta idea cobre mayor relevancia.
Predicción de su existencia
Debido al gran éxito de la electrodinámica cuántica para el caso de la interacción electromagnética en los años 50, los científicos intentaron desarrollar una teoría similar para la interacción débil. La teoría culminó con la aparición de la teoría que unifica el electromagnetismo con la interacción débil: la teoría electrodébil. Por su trabajo en la teoría electrodébil; Sheldon Glashow, Steven Weinberg, y Abdus Salam recibieron el premio Nobel de física.
La teoría electrodébil postuló entonces la existencia de los bosones W para explicar la desintegración beta, y también postuló la existencia del bosón Z y de la transferencia de momento por parte del mismo. El mayor problema que tuvo la teoría fue que los portadores tuvieran masa, al contrario que los demás que no la tienen. Una explicación, el mecanismo de Higgs, rompe la simetría de la teoría SU(2) (cuaternios reales) de gauge para dar masa a los bosones W y Z; y además predice la existencia del bosón de Higgs, causante de la masa de todas las partículas.
La combinación de dicha teoría de gauge, la interacción electromagnética y el mecanismo de Higgs recibe el nombre de modelo de Glashow-Weinberg-Salam. En el 2006, todo lo que este modelo describe está probado experimentalmente excepto la existencia del bosón de Higgs.
Cálculo de masas mediante el mecanismo de Higgs
Hacemos una aplicación directa del mecanismo de Higgs para resolver el problema de encontrar la masa de bosones vectoriales Z0 y W+-. Aplicamos al caso de la ruptura de simetría local no abeliana. Partimos de una lagrangiana que describe dos campos bosónicos escalares complejos:
donde el potencial V es:
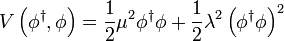 ,
,
la derivada covariante es:
y el tensor del campo abeliano
- Si μ2 > 0 la lagragiana describe la teoría de Yang-Mills.
- Si μ2 < 0, es el caso que nos interesa. La simetría SU(2) se rompe espontáneamente.
El mínimo de potencial vendrá dado por
Tomamos como vacío:
Expandimos el campo alrededor de φ0.
Parametrizamos la perturbación en términos de cuatro campos reales: tres ε(x) y un φ(x):
Como es invariante U(1), mediante una transformación
La libertad de elección de Gauge se usa para convertir φ en una componente de un isoespinor. La añadimos en la lagrangiana.
Reordenando los términos, el lagrangiano queda:
Ahora separamos los campos W3 y B e introduciendo el ángulo de Weinberg como:
llegamos a que:
El otro nuevo campo será
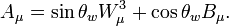 La lagrangiana:
La lagrangiana:Por fin tenemos un campo escalar masivo
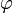 de Higgs, con masa
de Higgs, con masa 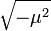 . Además hay tres bosones vectoriales masivos: W1, W2 y Z. Las masas son:
. Además hay tres bosones vectoriales masivos: W1, W2 y Z. Las masas son:Los generadores
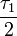 ,
,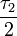 y
y 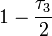 no dejan el vacio invariante. Pero
no dejan el vacio invariante. Pero 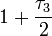 sí, y es el responsable de que deje el campo Aμ no tenga masa. El mecanismo de Higgs da masa a los bosones de Gauge, comiéndose tres de los cuatro campos de Higgs.
sí, y es el responsable de que deje el campo Aμ no tenga masa. El mecanismo de Higgs da masa a los bosones de Gauge, comiéndose tres de los cuatro campos de Higgs.Descubrimiento de los bosones
Su descubrimiento fue uno se sus mayores logros del CERN. Primero, el laboratorio descubrió muchos de los efectos que se previeron para éstos bosones; y después, en 1983, descubrió a las propias partículas.
Desde principios del siglo XX se conoce la desintegración beta, uno de los efectos más importantes de la interacción débil mediada por los bosones W. Se tuvo que esperar hasta 1973 para que la cámara de burbujas Gargamelle observara los efectos de la interacción de corriente neutra por parte de bosones Z, ya prevista por la reciente teoría electrodébil. Se fotografió como unos cuantos electrones comenzaron de pronto a moverse sin más. Éste hecho insólito se interpretó como el intercambio de un bosón Z por parte de una partícula no observada, un neutrino.
El descubrimiento propiamente dicho de los bosones tuvo que esperar 10 años, hasta la construcción del Super Proton Synchrotron. Entonces, se pudo demostrar la existencia de los bosones W y Z durante una serie de experimentos dirigidos por Carlo Rubbia y Simon van der Meer (los experimentos UA1 y UA2). Ambos científicos recibieron el premio Nobel de física en 1984 por su descubrimiento.
Véase también
- Modelo estándar
- Interacción nuclear débil
- Desintegración beta
Referencias
- ↑ «Precision measurement of W boson mass portends stricter limits for Higgs particle» (en inglés), traducción al español. Consultado el 13 de marzo de 2009.
Categoría: Bosones
Wikimedia foundation. 2010.

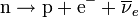
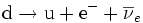
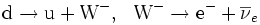
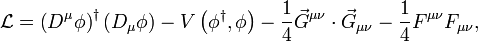
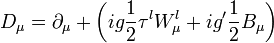
![F_{\mu\nu}=\partial_{\mu}B_{\nu}-\partial_{\nu}B_{\mu}\qquad ;\qquad G_{\mu\nu}=\partial_{\mu}W_{\nu}-\partial_{\nu}W_{\mu}+ig[W_{\mu},W_{\nu}]](/pictures/eswiki/51/331f71b075700a7464af5d53f9a15b05.png)
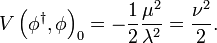
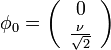
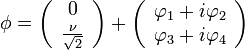
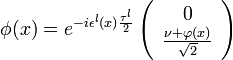
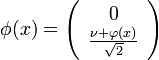
![\mathcal{L}=\left[\partial^{\mu}\phi^{\dagger}-\phi^{\dagger}\left(igW^{\mu}+i\frac{g'}{2}B^{\mu}\right)\right]\left[ \left( \partial_ {\mu}+igW_{\mu}+i\frac{g'}{2}B_{\mu}\right)\phi\right]-V\left(\phi^{\dagger}\phi\right)-\frac{1}{4}\vec{G}^{\mu\nu}\cdot\vec{G}_{\mu\nu}-\frac{1}{4}F^{\mu\nu}F_{\mu\nu}.](/pictures/eswiki/99/c1dc037cd82fd22b8003bec247f4cbb3.png)
![\mathcal{L}=\frac{1}{2}\left[\left(\partial^{\mu}\varphi\right)\left(\partial_{\mu}\varphi\right) +\mu^2\varphi^2 \right]-\frac{1}{4}\vec{G}^{\mu\nu}\cdot\vec{G}_{\mu\nu}-\frac{1}{4}F^{\mu\nu}F_{\mu\nu}+\frac{g^2}{8}\nu^2\left(W^{1\mu}W^1_{\mu}+W^{2\mu}W^2_{\mu}\right)+\frac{1}{8}\nu^2\left(gW^{3\mu}-g'B^{\mu}\right)\left(gW^{3}_{\mu}-g'B^{\mu}\right)+\mathcal{O}(.^2)+\Lambda](/pictures/eswiki/55/79be899a349c76296505e2b44541f3ed.png)
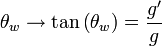
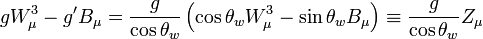
![\mathcal{L}=\frac{1}{2}\left[\left(\partial^{\mu}\varphi\right)\left(\partial_{\mu}\varphi\right) +\mu^2\varphi^2 \right]-\frac{1}{4}\sum_{i=1}^{2}{\left(\left(\partial^{\mu}W^{i\nu}- \partial^{\nu}W^{i\mu}\right)\left(\partial_{\mu}W^{i}_{\nu}- \partial_{\nu}W^{i}_{\mu}\right)-\frac{1}{2}g^2\nu^2W^{i\mu}W^i_{\mu}\right)}](/pictures/eswiki/50/20ad4bd37c0a62200280d8dd8dfd0cfd.png)