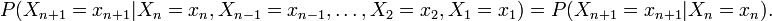Cadena de Márkov

Cadena de Márkov

Cadena de Márkov

Una cadena de Márkov, que recibe su nombre del matemático ruso Andrei Andreevitch Markov (1856-1922), es una serie de eventos, en la cual la probabilidad de que ocurra un evento depende del evento inmediato anterior. En efecto, las cadenas de este tipo tienen memoria. "Recuerdan" el último evento y esto condiciona las posibilidades de los eventos futuros. Esta dependencia del evento anterior distingue a las cadenas de Márkov de las series de eventos independientes, como tirar una moneda al aire o un dado.

Este tipo de proceso, introducido por Márkov en un artículo publicado en 1907,[1] presenta una forma de dependencia simple, pero muy útil en muchos modelos, entre las variables aleatorias que forman un proceso estocástico. En los negocios, las cadenas de Márkov se han utilizado para analizar los patrones de compra de los deudores morosos, para planear las necesidades de personal y para analizar el reemplazo de equipo.

Contenido

Definición formal

En matemáticas, se define como un proceso estocástico discreto que cumple con la propiedad de Márkov, es decir, si se conoce la historia del sistema hasta su instante actual, su estado presente resume toda la información relevante para describir en probabilidad su estado futuro.

Una cadena de Márkov es una secuencia X1, X2, X3,... de variables aleatorias. El rango de estas variables, es llamado espacio estado, el valor de Xn es el estado del proceso en el tiempo n. Si la distribución de probabilidad condicional de Xn+1 en estados pasados es una función de Xn por sí sola, entonces:

P(X_{n+1}=x_{n+1}|X_n=x_n, X_{n-1}=x_{n-1}, \ldots, X_2=x_2, X_1=x_1) = P(X_{n+1}=x_{n+1}|X_n=x_n). \,

Donde xi es el estado del proceso en el instante i. La identidad mostrada es la propiedad de Márkov.


Cadenas de Márkov en tiempo continuo

Si en lugar de considerar una secuencia discreta X1, X2,..., Xi,.. con i indexado en el conjunto 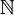\mathbb{N}\;\! de números naturales, se consideran las variables aleatorias Xt con t que varía en un intervalo continuo del conjunto 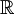\mathbb{R}\;\! de números reales, tendremos una cadena en tiempo continuo. Para este tipo de cadenas en tiempo continuo la propiedad de Márkov se expresa de la siguiente manera:

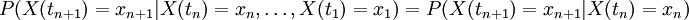P(X(t_{n+1})=x_{n+1} | X(t_n)=x_n, \ldots, X(t_1)=x_1) = P(X(t_{n+1})=x_{n+1}|X(t_n)=x_n) tal que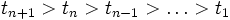 t_{n+1} > t_n > t_{n-1} > \dots > t_1

Referencias

  1. ↑ Basharin, Gely P. et al. (2004). «The Life and Work of A. A. Márkov». Elsevier.

Enlaces externos

Obtenido de "Cadena de M%C3%A1rkov"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Cadena de Markov — Una cadena de Markov, que recibe su nombre del matemático ruso Andrei Markov, es una serie de eventos, en la cual la probabilidad de que ocurra un evento determinado depende del evento inmediatamente anterior. En efecto, las cadenas de este tipo… …   Enciclopedia Universal

  • Modelo oculto de Márkov — Ejemplo de transición de estados en un modelo oculto de Márkov x estados ocultos y salidas observables a probabilidades de transición b probabilidades de salida Un modelo oculto de Márkov o HMM (por sus siglas del inglés, Hidden Markov Model) es… …   Wikipedia Español

  • Andréi Márkov — Andréi Márkov. Andréi Andréyevich Márkov (Андрей Андреевич Марков) (14 de junio de 1856 20 de julio de 1922) fue un matemático ruso conocido por sus trabajos en la teoría de los números y la teoría de probabilidades. Márkov nació en Riazán, Rusia …   Wikipedia Español

  • Propiedad de Márkov — Saltar a navegación, búsqueda Una cadena de Márkov se puede caracterizar por la probabilidad de ir al estado n+1 condicionada a que antes estábamos en el estado n: Que es la probabilidad de transición del proceso. La propiedad de las cadenas de… …   Wikipedia Español

  • Propiedad de Markov — Una cadena de Markov se puede caracterizar por la probabilidad de ir al estado n+1 condicionada a que antes estábamos en el estado n: Que es la probabilidad de transición del proceso. La propiedad de las cadenas de Markov es que las transiciones… …   Enciclopedia Universal

  • Algoritmo de cadena Lempel-Ziv-Markov — Saltar a navegación, búsqueda El algoritmo de cadena Lempel Ziv Markov (Lempel Ziv Markov chain Algorithm LZMA) es un algoritmo para la compresión de datos. Obtenido de Algoritmo de cadena Lempel Ziv Markov Categorías: Wikipedia:Infraesbozos |… …   Wikipedia Español

  • Georgi Markov — Georgi o Gueorgui Ivanov Markov, en búlgaro Георги Иванов Марков, (1 de marzo de 1929 11 de septiembre de 1978) fue un notable disidente búlgaro. Markov trabajó originalmente como un novelista y dramaturgo, pero en 1969, desertó de la entonces… …   Wikipedia Español

  • Autómata finito — Un autómata finito (AF) o máquina de estado finito es un modelo matemático que realiza cómputos en forma automática sobre una entrada para producir una salida. Este modelo está conformado por un alfabeto, un conjunto de estados y un conjunto de… …   Wikipedia Español

  • Ley de Chapman-Kolmogórov — La ley de Chapman Kolmogorov se basa en la ecuación del mismo nombre, a la que llegaron de forma independiente el matemático británico Sydney Chapman y el matemático ruso Andrey Kolmogorov. Enunciada de una forma sencilla dice: la probabilidad de …   Wikipedia Español

  • Anexo:Episodios de Numb3rs — La siguiente es una lista de episodios de la serie norteamericana NUMB3RS. Contenido 1 Estrenos y Lanzamientos en DVD 2 Primera temporada (2005) 3 Segunda temporada (2005 2006) …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”