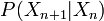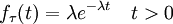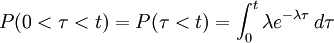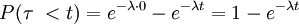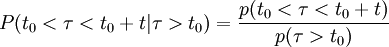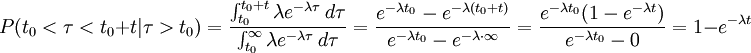Propiedad de Márkov

Propiedad de Márkov

Propiedad de Márkov

Una cadena de Márkov se puede caracterizar por la probabilidad de ir al estado n+1 condicionada a que antes estábamos en el estado n:

P(X_{n+1}|X_n) \,

Que es la probabilidad de transición del proceso. La propiedad de las cadenas de Márkov es que las transiciones entre los estados, sólo puede producirse entre estados vecinos. Sólo se puede llegar al estado i desde el estado i-1 ó bien de i+1.

Este tipo de estadística se suele encontrar en la distribución exponencial, cuya función de densidad de probabilidad se expresa así:

f_ \tau (t) = \lambda e^{-\lambda t} \quad t>0

Vamos a comprobar que un proceso definido por esta fdp no tiene memoria. La probabilidad de que haya una transición entre 0 y un tiempo t cualquiera es:

P(0< \tau < t) = P( \tau < t) = \int_{0}^{t} \lambda e^{-\lambda \tau} \, d\tau

Integrando obtenemos:

P(\tau\ < t)=e^{-\lambda \cdot 0} - e^{-\lambda t} = 1 - e^{-\lambda t}

Ahora vamos a calcular la probabilidad para el mismo intervalo t, pero con instante de inicio diferente t0. Calcularemos la probabilidad de tener una transición en el intervalo t, (de t0 hasta t0+t) condicionado a que antes de t0 no ha habido ninguna transición:

P(t_0< \tau < t_0+t | \tau > t_0) = \frac{p(t_0< \tau < t_0+t)}{p(\tau > t_0)}

Sustituyendo por las fdp y operando obtenemos:

P(t_0< \tau < t_0+t | \tau > t_0) = \frac{\int_{t_0}^{t_0+t} \lambda e^{-\lambda \tau} \, d\tau}{\int_{t_0}^{\infty} \lambda e^{-\lambda \tau} \, d\tau} = \frac {e^{-\lambda t_0} - e^{-\lambda (t_0+t)}}{e^{-\lambda t_0} - e^{-\lambda \cdot \infty}} = \frac {e^{-\lambda t_0} (1 - e^{-\lambda t})}{e^{-\lambda t_0}-0} = 1 - e^{-\lambda t}

Con lo que queda demostrado que la probabilidad de tener una transición en un estado, no depende del tiempo anterior.

Obtenido de "Propiedad de M%C3%A1rkov"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Propiedad de Markov — Una cadena de Markov se puede caracterizar por la probabilidad de ir al estado n+1 condicionada a que antes estábamos en el estado n: Que es la probabilidad de transición del proceso. La propiedad de las cadenas de Markov es que las transiciones… …   Enciclopedia Universal

  • Cadena de Márkov — Saltar a navegación, búsqueda Una cadena de Márkov, que recibe su nombre del matemático ruso Andrei Andreevitch Markov (1856 1922), es una serie de eventos, en la cual la probabilidad de que ocurra un evento depende del evento inmediato anterior …   Wikipedia Español

  • Modelo oculto de Márkov — Ejemplo de transición de estados en un modelo oculto de Márkov x estados ocultos y salidas observables a probabilidades de transición b probabilidades de salida Un modelo oculto de Márkov o HMM (por sus siglas del inglés, Hidden Markov Model) es… …   Wikipedia Español

  • Andréi Márkov — Andréi Márkov. Andréi Andréyevich Márkov (Андрей Андреевич Марков) (14 de junio de 1856 20 de julio de 1922) fue un matemático ruso conocido por sus trabajos en la teoría de los números y la teoría de probabilidades. Márkov nació en Riazán, Rusia …   Wikipedia Español

  • Camino aleatorio — Saltar a navegación, búsqueda Ejemplo de ocho caminos aleatorios en una dimensión empezando en 0. La gráfica muestra la posición actual sobre una linea (eje vertical) versus los intervalos de tiempo (eje horizontal). El camino aleatorio o paseo… …   Wikipedia Español

  • Campo aleatorio condicional — Un campo aleatorio condicional (Conditional Random Field o CRF en inglés) es un modelo estocástico utilizado habitualmente para etiquetar y segmentar secuencias de datos o extraer información de documentos. En algunos contextos también se les… …   Wikipedia Español

  • Ley de Chapman-Kolmogórov — La ley de Chapman Kolmogorov se basa en la ecuación del mismo nombre, a la que llegaron de forma independiente el matemático británico Sydney Chapman y el matemático ruso Andrey Kolmogorov. Enunciada de una forma sencilla dice: la probabilidad de …   Wikipedia Español

  • Hopfield (RNA) — Una red de Hopfield es una forma de red neuronal artificial recurrente inventada por John Hopfield. Las redes de Hopfield se usan como sistemas de Memoria asociativa con unidades binarias. Están diseñadas para converger a un mínimo local, pero la …   Wikipedia Español

  • Biología matemática — Saltar a navegación, búsqueda Biología Matemática o Biomatemática es una área interdisciplinaria de estudios que se enfoca en modelamiento de los procesos biológicos utilizando técnicas matemáticas. Tiene grandes aplicaciones teóricas y prácticas …   Wikipedia Español

  • Paco Montalvo — BIOGRAPHY Leo Brouwer, in 2009 wrote: Paco Montalvo is a genius. Paco Montalvo (Francisco Jose Montalvo) was born in Cordoba in 1992. At 11 months he picked up his first violin and literally started walking, giving his first recital at age 6. At… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”