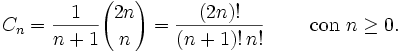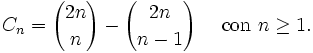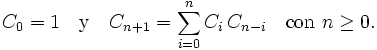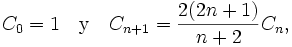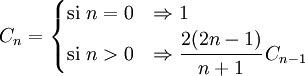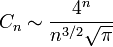Los números de catalán obtienen su nombre del matemático Eugène Charles Catalán (1814–1894) de origen belga. Se utilizan en combinatoria y estos son una secuencia de números naturales que aparecen en varios problemas de conteo, habitualmente recursivos. El n-ésimo número de catalán se obtiene, aplicando coeficientes binomiales, a partir de la siguiente fórmula:

Contenido 1 Propiedades 2 Programación 2.1 Código Recursivo 2.2 Código Dinámico 2.3 ¿Cómo Ejecutarlo en Java? 2.4 Limitaciones

Propiedades

Una expresión alternativa para Cn es:

Esta otra expresión muestra que Cn es un número natural, lo cual no resulta obvio a priori mirando la primera fórmula dada. Los números de catalán satisfacen la siguiente relación de recurrencia:

Y también satisfacen:

Que puede ser una forma más eficiente de calcularlos. La expresión en forma de recursión, seria:

Asintóticamente, los números de catalán crecen como:

Considerando que el cociente entre el n-ésimo número de catalán y la expresión de la derecha tiende hacia 1 cuando n → ∞ (esto puede probarse usando la fórmula de Stirling).

TABLA 1. Números en la serie Catalán

n	Cn	n	Cn
0	1	11	58.786
1	1	12	208.012
2	2	13	742.900
3	5	14	2.674.440
4	14	15	9.694.845
5	42	16	35.357.670
6	132	17	129.644.790
7	429	18	477.638.700
8	1.430	19	1.767.263.190
9	4.862	20	6.564.120.420
10	16.796

Programación

Si se observa la fórmula de recursión planteada matemáticamente:

Con base en ella se puede programar dicho ecuación modelándola algorítmicamente. Solo es fijarse en los límites tomados en la función catalán y además guiarse por los resultados de la TABLA 1. que presentan anteriormente para comprobar nuestros resultados.

En JAVA sería de la siguiente manera:

Código Recursivo

/**
 * @authors Alejandro León Aguilar - William Felipe Rojas
 * Colombia 2007
**/
public class Catalan {
            /**
            * @param double n este es el valor al cual le vamos a calcular la función catalán
            * @return double el número ya calculado
            */
        public double numerosCatalan (double n)
        {
             if (n==0) //Condicion de parada de la recursión 
             {
                   return 1;
             }                         
             
             return (2*((2*n)-1))/(n+1)*numerosCatalan (n-1);
             /*Acción recursiva donde halla el Cn de n de menor a mayor, según la fomula   
               matemática*/              
        }
}

¿Por que se declara double? En Java hay que tener mucho cuidado con esa declaración de variables. Especificamos double porque cuando hacemos la división necesitamos el valor con decimales (y cuantos más decimales mejor) para hallar Cn en esa posición con respecto a n y a C (n-1).

La Complejidad y el Orden de este algoritmo son:

T(n) = a
T(n) = b + T(n − 1)
T(2) = b + a
T(3) = 2b + a
T(4) = 3b + a

T(n) = (n − 1)b + a
O((n − 1)b + a) = n

Tiempo en cálculo de números

n	Cn (nanosegundos)
0	8785
5	13732
10	15477
15	18859
20	20485

El tiempo anterior se calculó mirando cuánto se demoraba el método en hacer el debido proceso con un número cualquiera.

Sin un enfoque recursivo, puede tomarse desde el enfoque de “La programación Dinámica”, donde se utiliza respectivamente una tabla que facilitará encontrar el resultado porque no repetirá cálculos innecesarios (como ocurre con la recursividad), sino que hará uso de dicha tabla para hallar los valores continuos hasta dar con el resultado.

Código Dinámico

 /**
 * @author Ray Williams Robinson Valiente
 * Cuba 2008
 */

#include <stdio.h>

#include <string.h>

using namespace std;

int * slide;

int n;

int main() {

	while (printf("Introduzca el término deseado de la serie o 0 para terminar...\n")
			&& scanf("%d", &n) && n) {

		slide = new int[n+1];

		memset (slide, 0, sizeof(*slide));

		slide[0] = 1;

		for (register int i = 1; i <= n; i++)

			slide[i] = (slide[i-1]*2*(2*i-1))/(i+1);

		printf("%d\n",slide[n]);

	}

	return 0;

}

La tabla se inicia en la posición 0 con 1, siguiendo la formula matemática, ya con este valor ingresado en la tabla podemos hallar el valor siguiente y así sucesivamente, cada valor nuevo hallado debe utilizar para su calculo el número hallado anteriormente y almacenado en la tabla, y este nuevo valor se introduce en la tabla.

La complejidad del algoritmo y el Orden

double n	+1
If (n==0)	+1
return 1	+1
double tabla[]=new	+1
tabla[0]=1	+1
while()	3n+1
return tabla[(int) n]	+1
T (n)= 3n+7
O(3n+7)= n

Tiempo en calculo de números

n	Cn (nanosegundos)
0	7875
5	15849
10	17375
15	18542
20	19318

El tiempo anterior se calculó mirando cuánto se demoraba el método en hacer el debido proceso con un número cualquiera.

¿Cómo Ejecutarlo en Java?

Para ejecutarlo en Java basta con solo crear otra clase con el main, allí se pide el número n al cual se le va a calcular el equivalente en la serie catalán este debe ser double. En este paso debe hacerse la respectiva excepción cuando ingresen letras en vez de números y a su vez, cuando ingresan números negativos. Se escoge cualquiera de los 2 métodos y se crea su clase. Se declara el objeto de la otra clase en el main y se manda al método el número n acabado de ingresar. Por último bastaría con imprimir el número catalán ya encontrado el cual lo retorna el método, allí solo es hacerle un cast (long) a la respuesta para que nos dé el número entero equivalente en la serie catalán.

¿Porqué long? Para poder dar respuestas muy grandes.

Limitaciones

En Java un limitante son los números demasiado grandes, entonces en los algoritmos anteriores si el número 'n' es muy grande, nuestro algoritmo puede no dar la respuesta más acertada.