Camino euleriano

Camino euleriano

Camino euleriano

Dado un grafo conexo y no dirigido 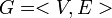G=<V,E>\, , P es un camino euleriano sobre G si y sólo si pasa por todas las aristas de G exáctamente una vez.

Teorema

Dado un grafo conexo y no dirigido 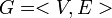G=<V,E>\, , si G tiene exactamente dos vértices de grado impar, entonces G tiene un camino euleriano.

Teorema

Dado un Grafo conexo y no orientado G; Si tiene 2k nodos de grado impar, entonces G puede ser escrito como unión de k caminos(simples) distintos sobre los arcos.

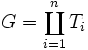G=\coprod_{i=1}^n T_i caminos distintos sobre los arcos

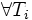\forall T_i va de un nodo de grado impar a un nodo de grado impar.

Un grafo admite un camino euleriano cuando tiene exactamente dos nodos de grado impar (conexos a los caminos)

Véase también

  • Ciclo Euleriano
Obtenido de "Camino euleriano"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Camino — Saltar a navegación, búsqueda Según el contexto, Camino puede referirse a: Contenido 1 Geografía 2 Literatura 3 Cine 4 Informática …   Wikipedia Español

  • Ciclo euleriano — Un ciclo euleriano es aquel camino que recorre todas las aristas de un grafo pasando una y sólo una vez por cada arco (arista) del grafo, siendo condición necesaria que regrese al vértice inicial de salida (ciclo = camino en un grafo donde… …   Wikipedia Español

  • Ciclo euleriano — Un ciclo euleriano es aquel camino que recorre todos los vértices (nodos) de un grafo pasando una y sólo una vez por cada arco (arista) del grafo y regresando al vértice de salida (ciclo = camino en un grafo donde coinciden vértice inicial o de… …   Enciclopedia Universal

  • Anexo:Glosario de teoría de grafos — Grafo simple no dirigido, con 6 vértices y 7 aristas. A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal correspondiente. Todos los… …   Wikipedia Español

  • Glosario en teoría de grafos — Anexo:Glosario en teoría de grafos Saltar a navegación, búsqueda Grafo con 6 nodos A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal …   Wikipedia Español

  • Grado (teoría de grafos) — Para otros usos de este término, véase Grado. Un grafo con vértices etiquetados según su grado. El vértice aislado se etiqueta con 0, pues su grado es igual a cero. En Teoría de grafos, el grado o valencia de un vértice es el número de aristas… …   Wikipedia Español

  • Grado (matemática) — Este ártículo trata del grado tal y como es empleado en el área de las matemáticas. Para significados alternativos de esta palabra, véase grado. En matemáticas existen diferentes significados de la palabra grado dependiendo del área matemática de …   Wikipedia Español

  • Grafo ciclo — Ciclo Cn C6: Un Grafo Ciclo de longitud 6. Vertices: n Aristas: n …   Wikipedia Español

  • Clases de complejidad P y NP — Diagrama de clases de complejidad para el caso en que P ≠ NP. La existencia de problemas fuera tanto de P como de NP completos en este caso fue determinada por Ladner.[1] La relación entre las clases de complejidad P …   Wikipedia Español

  • Leonhard Euler — Retrato de Leonhard Euler, pintado por Johann Georg Bruck …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”