Matriz de adyacencia

Matriz de adyacencia

La matriz de adyacencia es una matriz cuadrada que se utiliza como una forma de representar relaciones binarias.

Contenido

Construcción de la matriz a partir de un grafo

  1. Se crea una matriz cero, cuyas columnas y filas representan los nodos del grafo.
  2. Por cada arista que une a dos nodos, se suma 1 al valor que hay actualmente en la ubicación correspondiente de la matriz.
    Si tal arista es un bucle y el grafo es no dirigido, entonces se suma 2 en vez de 1.

Finalmente, se obtiene una matriz que representa el número de aristas (relaciones) entre cada par de nodos (elementos).

Existe una matriz de adyacencia única para cada grafo (sin considerar las permutaciones de filas o columnas), y viceversa.

Ejemplo de grafo no dirigido

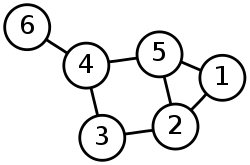Figura 1 Ejemplo de grafo no dirigido, para el que se calcula la matriz de adyacencia.

La matriz de adyacencia para el grafo no dirigido de la Figura 1 viene dada por:

\mathbf{A} = \begin{bmatrix} 0 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \end{bmatrix}

Ejemplo de grafo dirigido

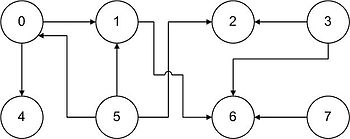Figura 2 Ejemplo de grafo dirigido, para el que se calcula la matriz de adyacencia.

La matriz de adyacencia para el grafo dirigido de la Figura 2 viene dada por:

\mathbf{A} = \begin{bmatrix} 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ \end{bmatrix}

Propiedades de la matriz de adyacencia

  • Para un grafo no dirigido la matriz de adyacencia es simétrica.
  • El número de caminos Ci,j(k), atravesando k aristas desde el nodo i al nodo j, viene dado por un elemento de la potencia k-ésima de la matriz de adyacencia:

C_{i,j}(k) = [\mathbf{A}^k]_{ij}

Comparación con otras representaciones

Existen otras formas de representar relaciones binarias, como por ejemplo los pares ordenados o los grafos. Cada representación tiene sus virtudes y desventajas.

En particular, la matriz de adyacencia es muy utilizada en la programación, porque su naturaleza binaria y matricial calza perfecto con la de los computadores. Sin embargo, a una persona común y corriente se le hará mucho más sencillo comprender una relación descrita mediante grafos, que mediante matrices de adyacencia.

Otra representación matricial para las relaciones binarias es la matriz de incidencia.

Aplicaciones

La relación entre un grafo y el vector y valor propio de su correspondiente matriz de adyacencia se estudian en la teoría espectral de grafos.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Matriz de distancias — En matemática, una matriz de distancias es una matriz cuyos elementos representan las distancias entre los puntos, tomados por pares, de un conjunto. Se trata, por lo tanto, de una matriz simétrica de tamaño NxN (dado un conjunto de N puntos en… …   Wikipedia Español

  • Matriz laplaciana — En teoría de grafos la matriz laplaciana también denominada matriz de admitancia o matriz de Kirchhoff es una representación matricial de un grafo. Otro tipo de representación matricial la proporciona la matriz de adyacencia, pero la matriz… …   Wikipedia Español

  • Matriz de incidencia — La matriz de incidencia es una matriz binaria (sus elementos sólo pueden ser unos o ceros), que se utiliza como una forma de representar relaciones binarias. Construcción de la matriz a partir de un grafo Relación binaria descrita mediante una… …   Wikipedia Español

  • Implementación del algoritmo de Floyd en Java — Saltar a navegación, búsqueda El algoritmo de Floyd intenta resolver el problema de encontrar el camino más corto entre todos los pares de nodos o vértices de un grafo. Esto es similar a construir una tabla con todas las distancias mínimas entre… …   Wikipedia Español

  • Teoría de grafos — Diagrama de un grafo con 6 vértices y 7 aristas. En matemáticas y en ciencias de la computación, la teoría de grafos (también llamada teoría de las gráficas) estudia las propiedades de los grafos (también llamadas gráficas). Un grafo es un… …   Wikipedia Español

  • Vector propio y valor propio — Fig. 1. En esta transformación de la Mona Lisa, la imagen se ha deformado de tal forma que su eje vertical no ha cambiado. (nota: se han recortado las esquinas en la imagen de la derecha) …   Wikipedia Español

  • Glosario en teoría de grafos — Anexo:Glosario en teoría de grafos Saltar a navegación, búsqueda Grafo con 6 nodos A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal …   Wikipedia Español

  • Anexo:Glosario de teoría de grafos — Grafo simple no dirigido, con 6 vértices y 7 aristas. A continuación se detallan los principales conceptos de la teoría de grafos. Para las definiciones formales o más detalladas, puede dirigirse al artículo principal correspondiente. Todos los… …   Wikipedia Español

  • Algoritmo de Prim — El algoritmo de Prim es un algoritmo perteneciente a la teoría de los grafos para encontrar un árbol recubridor mínimo en un grafo conexo, no dirigido y cuyas aristas están etiquetadas. En otras palabras, el algoritmo encuentra un subconjunto de… …   Wikipedia Español

  • Algoritmo de Floyd-Warshall — En informática, el algoritmo de Floyd Warshall, descrito en 1959 por Bernard Roy, es un algoritmo de análisis sobre grafos para encontrar el camino mínimo en grafos dirigidos ponderados. El algoritmo encuentra el camino entre todos los pares de… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”